题目内容
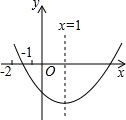 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b2-4ac>0;②abc<0;③8a+c>0;④9a+3b+c<0.
请你将正确结论的番号都写出来
考点:二次函数图象与系数的关系
专题:数形结合
分析:根据抛物线与x轴的交点个数可对①进行判断;由抛物线开口方向得到a>0,由抛物线的对称轴方程得到b=-2a<0,由抛物线与y轴的交点在x轴下方得到c<0,则可对②进行判断;由x=-2得4a-2b+c>0,再把b=-2a代入可得8a+c>0,于是可对③进行判断;利用抛物线的对称性得到抛物线与x的另一个交点在(3,0)与(4,0)之间,则x=3时,y<0,于是可对④进行判断.
解答:解:∵抛物线与x轴有2个交点,
∴△=b2-4ac>0,所以①正确;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-
=1,
∴b=-2a<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以②错误;
∵x=-2时,y>0,
∴4a-2b+c>0,
而b=-2a,
∴4a+4a+c>0,即8a+c>0,所以③正确;
∵抛物线与x的一个交点在(-2,0)与(-1,0)之间,
而对称轴为直线x=1,
∴抛物线与x的另一个交点在(3,0)与(4,0)之间,
∴x=3时,y<0,
∴9a+32b+c<0,所以④正确.
故答案为①④⑤.
∴△=b2-4ac>0,所以①正确;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=-
| b |
| 2a |
∴b=-2a<0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc>0,所以②错误;
∵x=-2时,y>0,
∴4a-2b+c>0,
而b=-2a,
∴4a+4a+c>0,即8a+c>0,所以③正确;
∵抛物线与x的一个交点在(-2,0)与(-1,0)之间,
而对称轴为直线x=1,
∴抛物线与x的另一个交点在(3,0)与(4,0)之间,
∴x=3时,y<0,
∴9a+32b+c<0,所以④正确.
故答案为①④⑤.
点评:本题考查了二次函数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c).抛物线与x轴交点个数由△决定:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知等腰三角形的腰长为10,底边长12,则底边上的高是( )
| A、6 | B、8 | C、10 | D、12 |
 如图,已知AC∥BD,OA=OC,则下列结论不成立的是( )
如图,已知AC∥BD,OA=OC,则下列结论不成立的是( )| A、∠B=∠C |
| B、∠A=∠D |
| C、∠AOC=∠BOD |
| D、OA=OB |
 如图,在△ABC中,DE∥BC,AD=1,DB=2,DE=2,则BC=( )
如图,在△ABC中,DE∥BC,AD=1,DB=2,DE=2,则BC=( )| A、2 | B、4 | C、6 | D、8 |
 如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为
如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB的度数为 如图,数轴上表示1,
如图,数轴上表示1,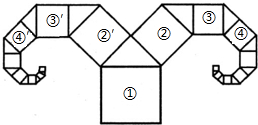 如图所示是一种“羊头”形图案,其作法是:从正方形①开始,以它的一条边为斜边作等腰直角三角形,然后再以这个等腰直角三角形两直角边为边作正方形②和②′,如此继续下去…,若正方形①的面积为a,则正方形⑦的边长是多少?正方形
如图所示是一种“羊头”形图案,其作法是:从正方形①开始,以它的一条边为斜边作等腰直角三角形,然后再以这个等腰直角三角形两直角边为边作正方形②和②′,如此继续下去…,若正方形①的面积为a,则正方形⑦的边长是多少?正方形 的边长是多少?
的边长是多少?