题目内容
一个正三角形和一个正六边形的周长相等，则它们的面积比为 ．
考点：正多边形和圆
专题：
分析：根据正多边形的面积等于周长与边心距的乘积的一半，所以只需根据它们的周长计算其边心距；在由正多边形的半径、边心距和边长组成的直角三角形中，根据锐角三角函数的概念可以分别求得它们的边心距，再进一步计算其面积，从而得到其比值．
解答：解：设它们的周长是1．根据题意，得
正三角形的边长是
，正六边形的边长是
．
则正三角形的边心距是
，正六边形的边心距是
．
则正三角形的面积是
，正六边形的面积是
．
则它们的面积比是
：
=2：3．
故答案为：2：3．
正三角形的边长是
| 1 |
| 3 |
| 1 |
| 6 |
则正三角形的边心距是
| ||
| 6 |
| ||
| 12 |
则正三角形的面积是
| ||
| 36 |
| ||
| 24 |
则它们的面积比是
| ||
| 36 |
| ||
| 24 |
故答案为：2：3．
点评：本题考查了正多边形和圆的有关知识，熟悉正多边形的面积公式：正多边形的面积等于周长与边心距的乘积的一半．能够根据由半径、边心距和半边组成的直角三角形，运用锐角三角函数进行计算是解题关键．
练习册系列答案
名师点拨卷系列答案
相关题目
下列四个交通标志图形中，不是轴对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
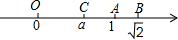如图，数轴上表示1，
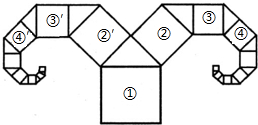如图所示是一种“羊头”形图案，其作法是：从正方形①开始，以它的一条边为斜边作等腰直角三角形，然后再以这个等腰直角三角形两直角边为边作正方形②和②′，如此继续下去…，若正方形①的面积为a，则正方形⑦的边长是多少？正方形
的边长是多少？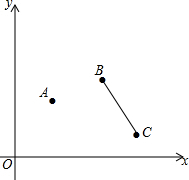
平面直角坐标系中，已知：A（2，3），B（4，4），C（5，1），在x轴上找一点D，使四边形ABCD的周长最小．
在4×4网格中，∠α的位置如图所示，则tanα的值为（ ）A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|