题目内容
18.关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0有两个不相等的实数根,则m的取值范围是( )| A. | m<2 | B. | m>$\frac{5}{4}$且m≠2 | C. | m≤2 | D. | m≥$\frac{5}{4}$且m≠2 |
分析 因为关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0有两个不相等的实数根,所以△=b2-4ac>0,从而可以列出关于m的不等式,求解即可,还要考虑二次项的系数不能为0.
解答 解:∵关于x的一元二次方程(m-2)2x2+(2m+1)x+1=0有两个不相等的实数根,
∴△=b2-4ac>0,即(2m+1)2-4×(m-2)2×1>0,
解这个不等式得,m>$\frac{5}{4}$,
又∵二次项系数是(m-2)2,
∴m≠2,
故M得取值范围是m>$\frac{5}{4}$且m≠2.
故选:B.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
8.弹簧挂上物体后会伸长(物体重量在0~10千克范围内),测得一弹簧的长度y(厘米)与所挂物体的质量x(千克)有如下关系:
(1)此弹簧的原长度是12厘米;
(2)物体每增加一千克重量弹簧伸长0.5厘米;
(3)弹簧总长度y(厘米)与所挂物体的重量x(千克)的函数关系式是y=0.5x+12.
| x(千克) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y(厘米) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
(2)物体每增加一千克重量弹簧伸长0.5厘米;
(3)弹簧总长度y(厘米)与所挂物体的重量x(千克)的函数关系式是y=0.5x+12.
10. 如图,在下面的立方体中,它的主视图是( )
如图,在下面的立方体中,它的主视图是( )
 如图,在下面的立方体中,它的主视图是( )
如图,在下面的立方体中,它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图是一个有多个相同小正方体堆积而成的几何体,该几何体的左视图是( )
如图是一个有多个相同小正方体堆积而成的几何体,该几何体的左视图是( )



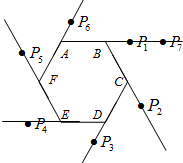 将正六边形ABCDEF的各边按如图所示延长,从射线AB开始分别在各射线上标记点P1、P2、P3、…,按此规律,点P2013在射线CD上.
将正六边形ABCDEF的各边按如图所示延长,从射线AB开始分别在各射线上标记点P1、P2、P3、…,按此规律,点P2013在射线CD上.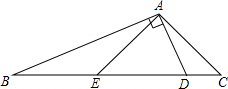 如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.若BD=13,则AC=6.5.
如图,在△ABC中,∠C=2∠B,D是BC上的一点,且AD⊥AB,点E是BD的中点,连结AE.若BD=13,则AC=6.5.