题目内容
4.化简:(1)(a-2b)2-(2a+b)(b-2a)-4a(a-b)
(2)$\frac{{a}^{2}+4ab+{4b}^{2}}{a-b}$÷($\frac{{3b}^{2}}{a-b}$-a-b)
分析 (1)原式利用完全平方公式,平方差公式,以及单项式乘以多项式法则计算,去括号合并即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=a2-4ab+4b2-b2+4a2-4a2+4ab=a2+3b2;
(2)原式=$\frac{(a+2b)^{2}}{a-b}$÷$\frac{3{b}^{2}-{a}^{2}+{b}^{2}}{a-b}$=$\frac{(a+2b)^{2}}{a-b}$•$\frac{a-b}{(2b+a)(2b-a)}$=$\frac{a+2b}{2b-a}$.
点评 此题考查了分式的混合运算,以及整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
14.若一个角的补角比这个角的余角的2倍多20°15′,则这个角的余角的度数是( )
| A. | 20°15′ | B. | 70°45′ | C. | 69°85′ | D. | 69°45′ |
15. 边长是m的正方形面积是7,如图,表示m的点在数轴上表示时,在哪两个字母之间( )
边长是m的正方形面积是7,如图,表示m的点在数轴上表示时,在哪两个字母之间( )
 边长是m的正方形面积是7,如图,表示m的点在数轴上表示时,在哪两个字母之间( )
边长是m的正方形面积是7,如图,表示m的点在数轴上表示时,在哪两个字母之间( )| A. | C与D | B. | A与B | C. | A与C | D. | B与C |
12.不等式组$\left\{\begin{array}{l}{2(x-1)>x}\\{x≤\frac{x+3}{2}}\end{array}\right.$的解是$\frac{1}{2}$<x≤3.
19.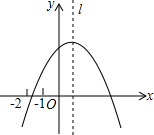 如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:①ac>0;②b2-4ac>0;③a+c<2-b;④a<-$\frac{1}{4}$;⑤x=-5和x=7时函数值相等.其中错误的结论有( )
如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:①ac>0;②b2-4ac>0;③a+c<2-b;④a<-$\frac{1}{4}$;⑤x=-5和x=7时函数值相等.其中错误的结论有( )
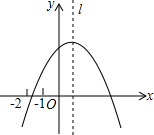 如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:①ac>0;②b2-4ac>0;③a+c<2-b;④a<-$\frac{1}{4}$;⑤x=-5和x=7时函数值相等.其中错误的结论有( )
如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:①ac>0;②b2-4ac>0;③a+c<2-b;④a<-$\frac{1}{4}$;⑤x=-5和x=7时函数值相等.其中错误的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.若代数式2a2-a+3的值为5,则代数式4a2-2a+6的值为( )
| A. | -22 | B. | 10 | C. | -10 | D. | 22 |