题目内容
11.如图1,在折线ABCDE中,AB∥DE,(1)①如果∠B=20°,∠C=60°,则∠D=140°;
②如果∠B=18°,∠D=135°,则∠C=63°;
(2)从(1)的结果你能发现∠B,∠C和∠D之间满足怎样的数列关系吗?请写出这个关系式,并加以说明;
(3)在图2的折线ABCDEF中,AB∥EF,请直接写出∠B,∠C,∠D和∠E所满足的关系式:∠D+∠C-∠B=∠E.
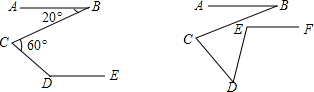
分析 (1)①过C作CF∥AB,根据AB∥DE可得出CF∥DE,再由平行线的性质即可得出结论;
②过程同①;
(2)延长FE交BC于点I,过点C作CH∥EF,根据AB∥EF得出∠B=∠BIE.再由CH∥EF可知∠BIE=∠BCH,∠FEH=∠CHE,故∠B=∠BCH.由三角形外角的性质即可得出结论.
解答 解:(1)①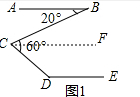 如图1,过C作CF∥AB,
如图1,过C作CF∥AB,
∵AB∥DE,
∴CF∥DE,
∴∠B=∠BCF,∠FCD+∠D=180°,
∵∠B=20°,
∴∠BCF=20°,
∴∠FCD=40°,
∴∠D=140°,
故答案为:140°;
②∵∠B=∠BCF,∠FCD+∠D=180°,
∴∠BCF=18°,∠FCD=180°-∠D=45°,
∴∠BCD=63°,
故答案为:63°;
(2)∠C+∠D-∠B=180°,
如图1,∵AB∥CF∥DE,
∴∠BCF=∠B,∠FCD+∠D=180°,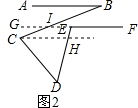
∴∠B+∠FCD=∠BCF+180°-∠D=∠BCD,
∴∠C+∠D-∠B=180°;
(3)延长FE交BC于点I,过点C作CH∥EF,
∵AB∥EF,
∴∠B=∠BIE.
∵CH∥EF,
∴∠BIE=∠BCH,∠FEH=∠CHE,
∴∠B=∠BCH.
∵∠D+∠DCH=∠CHE,
∴∠D+(∠BCD-∠B)=∠FEH,即∠D+∠C-∠B=∠E.
故答案为:∠D+∠C-∠B=∠E.
点评 本题考查的是平行线的性质,根据题意作出平行线,利用平行线的性质求解是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.关于x的方程kx2-3x-1=0有实根,则k的取值范围是( )
| A. | k$≤-\frac{9}{4}$ | B. | k$≥-\frac{9}{4}$且k≠0 | C. | k$≥-\frac{9}{4}$ | D. | k>$-\frac{9}{4}$且k≠0 |
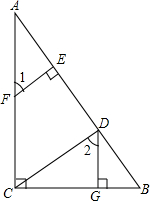 如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,将下列证明EF∥CD的过程及理由填写完整.
如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,将下列证明EF∥CD的过程及理由填写完整. 如图,一段河坝的横截面为梯形ABCD,根据图中数据,可知底宽AD=7.5+4$\sqrt{3}$(单位:m).
如图,一段河坝的横截面为梯形ABCD,根据图中数据,可知底宽AD=7.5+4$\sqrt{3}$(单位:m).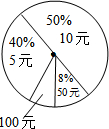 在江油市团委发起的“感恩河南”活动中,某班50名同学响应号召纷纷捐出零花钱,若不同捐款金额的人数百分比统计如图所示,则该班同学平均每人捐款13元.
在江油市团委发起的“感恩河南”活动中,某班50名同学响应号召纷纷捐出零花钱,若不同捐款金额的人数百分比统计如图所示,则该班同学平均每人捐款13元. 如图,A、B、C三点在数轴上,点C在点A与点B之间,且AC:BC=1:5.
如图,A、B、C三点在数轴上,点C在点A与点B之间,且AC:BC=1:5.