题目内容
7. 如图,在Rt△ABC中,∠C=90°,∠BAC=2∠B,AD是∠BAC的平分线,请说明CD与BC的数量关系.
如图,在Rt△ABC中,∠C=90°,∠BAC=2∠B,AD是∠BAC的平分线,请说明CD与BC的数量关系.
分析 由直角三角形的性质和已知条件求出∠B=30°,∠BAC=60°,由角平分线得出∠CAD=∠BAD=30°=∠B,由含30°角的直角三角形的性质得出CD=$\frac{1}{2}$AD,证出AD=BD,即可得出结论.
解答 解:BC=3CD;理由如下:
∵∠C=90°,
∴∠BAC+∠B=90°,
∵∠BAC=2∠B,
∴2∠B+∠B=90°,
∴∠B=30°,∠BAC=60°,
∵AD是∠BAC的平分线,
∴∠CAD=∠BAD=30°=∠B,
∴CD=$\frac{1}{2}$AD,AD=BD,
∴BD=2CD,
∴BC=3CD.
点评 本题考查了角平分线、含30°角的直角三角形的性质、等腰三角形的判定;熟练掌握含30°角的直角三角形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
19.甲、乙两同学同时从学校去火车站,已知学校到火车站的路程是a km,甲骑自行车b h到达,乙骑摩托车,比甲提前20min到达火车站,则甲、乙两人的平均速度之比为( )
| A. | $\frac{a}{b}$ | B. | $\frac{3b}{2}$ | C. | $\frac{3b-1}{3b}$ | D. | 以上均错 |
 如图,CD、AE为△ABC的高,∠B=45°,AC=4,求DE的长.
如图,CD、AE为△ABC的高,∠B=45°,AC=4,求DE的长.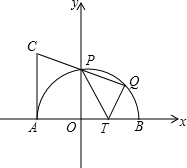 如图,在平面直角坐标系中,半径为2的半圆O与x轴交于A、B两点,与y轴交于点P,T是OB上的一点,OT=a(0<a<2),过A作AC⊥AB,且AC=AT,连接CP并延长交半圆于另一点Q,且Q恰为弧PB中点.
如图,在平面直角坐标系中,半径为2的半圆O与x轴交于A、B两点,与y轴交于点P,T是OB上的一点,OT=a(0<a<2),过A作AC⊥AB,且AC=AT,连接CP并延长交半圆于另一点Q,且Q恰为弧PB中点.