题目内容
 如图,点P,Q分别是∠AOB的边OA,OB上的点.
如图,点P,Q分别是∠AOB的边OA,OB上的点.(1)过点P画直线PD∥OB;(要求把经过的格点标出,只要一个)
(2)过点P画OB的垂线,垂足为H;过点Q画OA的垂线,交OA于点C,连接PQ;(要求同(1))
(3)线段QC的长度是点Q到
考点:作图—基本作图,垂线段最短,点到直线的距离
专题:
分析:(1)根据平行四边形的性质作图;
(2)根据正方形的性质作图;
(3)根据点到直线的距离、两点间的距离、垂线段最短等解答.
(2)根据正方形的性质作图;
(3)根据点到直线的距离、两点间的距离、垂线段最短等解答.
解答: 解:(1)如图(1),PD∥OB.
解:(1)如图(1),PD∥OB.
理由:∵QD∥OP,QD=OP,
∴四边形QOPD为平行四边形,
∴PD∥OB;
(2)如图(2),作PS交OB于H.理由:在正方形SRNQ中,对角线互相垂直.
(3)线段QC的长度是点Q到点O的距离,点P到OB的垂线段的长度是点P到直线OB的距离,线段PQ、PH的大小关系是 PQ> PH(用“<”号连接).理由是垂线段最短.
PH(用“<”号连接).理由是垂线段最短.
故答案为:点O,点P到OB的垂线段,PQ>PH,垂线段最短.
 解:(1)如图(1),PD∥OB.
解:(1)如图(1),PD∥OB.理由:∵QD∥OP,QD=OP,
∴四边形QOPD为平行四边形,
∴PD∥OB;
(2)如图(2),作PS交OB于H.理由:在正方形SRNQ中,对角线互相垂直.
(3)线段QC的长度是点Q到点O的距离,点P到OB的垂线段的长度是点P到直线OB的距离,线段PQ、PH的大小关系是 PQ>
 PH(用“<”号连接).理由是垂线段最短.
PH(用“<”号连接).理由是垂线段最短.故答案为:点O,点P到OB的垂线段,PQ>PH,垂线段最短.
点评:本题考查了作图--基本作图,要利用网格的特点,结合平行四边形的性质、正方形的性质解答.

练习册系列答案
相关题目
已知:∠AOB=60°,OC为∠AOB内部一条射线,OM,ON分别平分∠AOC,∠BOC,则∠MON的度数为( )
| A、30° | B、40° |
| C、45° | D、50° |
下面是我们熟悉的四个银行标志图形,不是轴对称的是( )
A、 |
B、 |
C、 |
D、 |
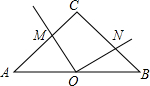 等腰直角△ABC中,∠C=90°,O是AB的中点,∠MON=90°,AC=12.求四边形OMCN的面积.
等腰直角△ABC中,∠C=90°,O是AB的中点,∠MON=90°,AC=12.求四边形OMCN的面积. 已知在△ABC中,∠ABC=∠ACB,∠1=∠2,求证:AD平分∠BAC.
已知在△ABC中,∠ABC=∠ACB,∠1=∠2,求证:AD平分∠BAC. 如图,△ABC中,AD是BC边上的高,CE是AB边上的中线,且DC=AE,G是CE的中点,连结DG.
如图,△ABC中,AD是BC边上的高,CE是AB边上的中线,且DC=AE,G是CE的中点,连结DG. 如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,则
如图,△ABC中,点D、E分别为AB、AC的中点,连接DE,线段BE、CD相交于点O,则