题目内容
 如图,△ABC中,AD是BC边上的高,CE是AB边上的中线,且DC=AE,G是CE的中点,连结DG.
如图,△ABC中,AD是BC边上的高,CE是AB边上的中线,且DC=AE,G是CE的中点,连结DG.(1)求证:DG⊥CE;
(2)作∠BEC的角平分线交BC于F,求证:BE+BF=EC.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)连接DE,易证AE=DE,即可求得CD=DE,根据等腰三角形底边三线合一性质即可解题;
(2)延长CB到H使BH=BE,连接EH,易证AE=BE=DE=DC和∠CDE=∠EBH,即可证明△CDE≌△EBH,可得∠DCE=∠BEH,EC=EH,再根据EF是∠BEC的角平分线,可求得∠EFH=∠FEH,即可求得EH=FH,即可解题.
(2)延长CB到H使BH=BE,连接EH,易证AE=BE=DE=DC和∠CDE=∠EBH,即可证明△CDE≌△EBH,可得∠DCE=∠BEH,EC=EH,再根据EF是∠BEC的角平分线,可求得∠EFH=∠FEH,即可求得EH=FH,即可解题.
解答:证明:(1)连接DE,
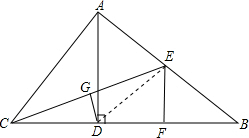
∵RT△ABD中,E是AB中点,
∴AE=DE,
∵CD=AE,
∴CD=DE,
∵G是CE中点,
∴DG⊥CE;
(2)延长CB到H使BH=BE,连接EH,
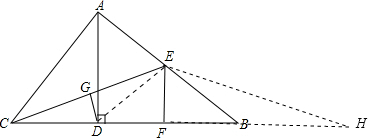
∵AD是BC边上的高,CE是AB边上的中线,
∴RT△ADB中AE=BE=DE,
∵DC=AE,
∴AE=BE=DE=DC,
∴∠BDE=∠DBE,
∵∠BDE+∠CDE=∠DBE+∠EBH=180°,
∴∠CDE=∠EBH,
在△CDE和△EBH中,
,
∴△CDE≌△EBH(SAS),
∴∠DCE=∠BEH,EC=EH,
∵∠EFH=∠DCE+∠CEF,∠FEH=∠BEH+∠BEF,
∵EF是∠BEC的角平分线,
∴∠CEF=∠BEF,
∴∠EFH=∠FEH,
∴EH=FH,
∵FH=BH+BF=BE+BF,
∴BE+BF=EC.

∵RT△ABD中,E是AB中点,
∴AE=DE,
∵CD=AE,
∴CD=DE,
∵G是CE中点,
∴DG⊥CE;
(2)延长CB到H使BH=BE,连接EH,

∵AD是BC边上的高,CE是AB边上的中线,
∴RT△ADB中AE=BE=DE,
∵DC=AE,
∴AE=BE=DE=DC,
∴∠BDE=∠DBE,
∵∠BDE+∠CDE=∠DBE+∠EBH=180°,
∴∠CDE=∠EBH,
在△CDE和△EBH中,
|
∴△CDE≌△EBH(SAS),
∴∠DCE=∠BEH,EC=EH,
∵∠EFH=∠DCE+∠CEF,∠FEH=∠BEH+∠BEF,
∵EF是∠BEC的角平分线,
∴∠CEF=∠BEF,
∴∠EFH=∠FEH,
∴EH=FH,
∵FH=BH+BF=BE+BF,
∴BE+BF=EC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,考查了等腰三角形底边三线合一的性质,本题中求证△CDE≌△EBH是解题的关键.

练习册系列答案
相关题目

 如图,已知AD=
如图,已知AD= 如图,点P,Q分别是∠AOB的边OA,OB上的点.
如图,点P,Q分别是∠AOB的边OA,OB上的点.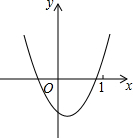 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论①ac<0,②当x>1时,a+b+c>0,③a-b+c>0,其中正确的个数为
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论①ac<0,②当x>1时,a+b+c>0,③a-b+c>0,其中正确的个数为


