题目内容
 已知在△ABC中,∠ABC=∠ACB,∠1=∠2,求证:AD平分∠BAC.
已知在△ABC中,∠ABC=∠ACB,∠1=∠2,求证:AD平分∠BAC.考点:全等三角形的判定与性质
专题:证明题
分析:易证AB=AC和BD=CD,即可证明△ABD≌△ACD,可得∠BAD=∠CAD,即可解题.
解答:证明:∵∠ABC=∠ACB,
∴AB=AC,
∵∠1=∠2,
∴BD=CD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AD平分∠BAC.
∴AB=AC,
∵∠1=∠2,
∴BD=CD,
在△ABD和△ACD中,
|
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∴AD平分∠BAC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABD≌△ACD是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
在数轴上表示不等式组
的解,其中正确的是( )
|
A、 |
B、 |
C、 |
D、 |
下列语句错误的是( )
| A、任何数的绝对值都是非负数 |
| B、有公共端点的两条射线组成的图形叫做角 |
| C、任何数都有倒数 |
| D、经过两点有且只有一条直线 |

 如图,点P,Q分别是∠AOB的边OA,OB上的点.
如图,点P,Q分别是∠AOB的边OA,OB上的点.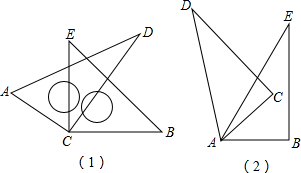 如图(1),将两块直角三角尺的直角顶点C叠放在一起,
如图(1),将两块直角三角尺的直角顶点C叠放在一起,