题目内容
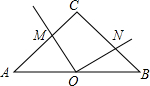 等腰直角△ABC中,∠C=90°,O是AB的中点,∠MON=90°,AC=12.求四边形OMCN的面积.
等腰直角△ABC中,∠C=90°,O是AB的中点,∠MON=90°,AC=12.求四边形OMCN的面积.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:连接OC,易证OA=OC=OB,∠ACO=∠ABC=45°,∠COM=∠BON,即可证明△COM≌△BON,可得四边形OMCN的面积=S△AOC,根据AC可以求得AO的值,即可解题.
解答:解:连接OC,
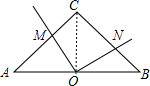
∵等腰直角△ABC中,∠C=90°,
∴OA=OC=OB,∠ACO=∠ABC=45°,
∵∠COM+∠CON=90°,∠CON+∠BON=90°,
∴∠COM=∠BON,
在△COM和△BON中,
,
∴△COM≌△BON(ASA),
∴四边形OMCN的面积=S△AOC,
∵AC=12,
∴AO=CO=6
,
∴四边形OMCN的面积=S△AOC=
AO•CO=36.

∵等腰直角△ABC中,∠C=90°,
∴OA=OC=OB,∠ACO=∠ABC=45°,
∵∠COM+∠CON=90°,∠CON+∠BON=90°,
∴∠COM=∠BON,
在△COM和△BON中,
|
∴△COM≌△BON(ASA),
∴四边形OMCN的面积=S△AOC,
∵AC=12,
∴AO=CO=6
| 2 |
∴四边形OMCN的面积=S△AOC=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形面积相等的性质,本题中求证△COM≌△BON是解题的关键.

练习册系列答案
相关题目
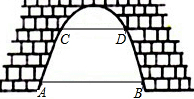 如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
如图,有一座抛物线形拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m,就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶. 如图,点P,Q分别是∠AOB的边OA,OB上的点.
如图,点P,Q分别是∠AOB的边OA,OB上的点.