Question

6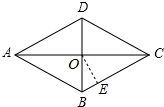．如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=16，BD=12，OE⊥BC，垂足为点E，则OE=4.8．

Answer 1

分析 首先证明△BOC是直角三角形，利用面积法即$\frac{1}{2}$•CB•OE=$\frac{1}{2}$•OB•OC，即可解决问题．

解答 解：如图，∵四边形ABCD是菱形，
∴AC⊥BD，AO=OC=8，OD=OB=6，
∴在RT△BOC中，
∵∠BOC=90°，OC=8，OB=6，
∴BC=$\sqrt{O{C}^{2}+O{B}^{2}}$=10，
∵OE⊥BC，
∴$\frac{1}{2}$•CB•OE=$\frac{1}{2}$•OB•OC，
∴OE=$\frac{OB•OC}{BC}$=4.8．
故答案为4.8．

点评 本题考查菱形的性质，勾股定理等知识，解题的关键是学会利用面积法求直角三角形斜边上的高，属于基础题，中考常考题型．