题目内容
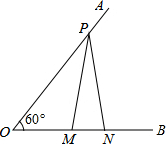 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM=考点:勾股定理,等腰三角形的性质,含30度角的直角三角形
专题:
分析:过P作PD⊥OB,交OB于点D,在直角三角形POD中,利用锐角三角函数定义求出OD的长,再由PM=PN,利用三线合一得到D为MN中点,根据MN求出MD的长,由OD-MD即可求出OM的长.
解答: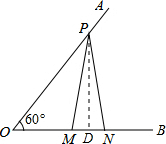 解:过P作PD⊥OB,交OB于点D,
解:过P作PD⊥OB,交OB于点D,
在Rt△OPD中,cos60°=
=
,OP=12,
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=
MN=1,
∴OM=OD-MD=6-1=5.
故答案为:5.
 解:过P作PD⊥OB,交OB于点D,
解:过P作PD⊥OB,交OB于点D,在Rt△OPD中,cos60°=
| OD |
| OP |
| 1 |
| 2 |
∴OD=6,
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=
| 1 |
| 2 |
∴OM=OD-MD=6-1=5.
故答案为:5.
点评:此题考查的是勾股定理,含30度直角三角形的性质,等腰三角形的性质等知识,熟练掌握直角三角形的性质是解本题的关键.

练习册系列答案
相关题目
关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根为0,则a的值为( )
| A、1或-1 | B、-1 | C、1 | D、0 |
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )
直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )| A、3 | B、3.5 | C、3.75 | D、4 |
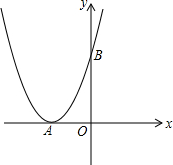 如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.
如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.