题目内容
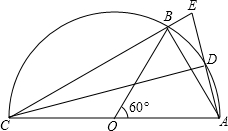 如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.
如图,AC是半圆O的直径,B是半圆上的一点,D是弧AB的中点,连接AB、CB、CD、AD,延长AD交CB的延长线于点E.(1)求证:CA=CE;
(2)若∠AOB=60°,AE2=24(2-
| 3 |
考点:圆的综合题
专题:
分析:(1)由AC是半圆O的直径得到∠ADC=90°,由D是弧AB的中点得到∠ACD=∠BCD,再利用ASA证明△ACD≌△ECD,根据全等三角形的对应边相等即可得到CA=CE;
(2)先根据有一个角为60°的三角形是等边三角形得出△AOB是等边三角形,由等边三角形的性质得到AB=OA=OB,∠OAB=60°,再由两角对应相等的两三角形相似得到△CDE∽△ABE,根据相似三角形对应边成比例得出DE:BE=CE:AE,将DE=
AE,CE=2AB代入,得到AE2=4BE•AB,又在△ABE中,运用勾股定理得出AB2+BE2=AE2,将AE2=24(2-
)分别代入上面两个式子,求出AB的值,然后根据圆的面积根据即可得出半圆O的面积.
(2)先根据有一个角为60°的三角形是等边三角形得出△AOB是等边三角形,由等边三角形的性质得到AB=OA=OB,∠OAB=60°,再由两角对应相等的两三角形相似得到△CDE∽△ABE,根据相似三角形对应边成比例得出DE:BE=CE:AE,将DE=
| 1 |
| 2 |
| 3 |
解答:(1)证明:∵AC是半圆O的直径,
∴∠ADC=90°.
∵D是弧AB的中点,
∴
=
,
∴∠ACD=∠BCD.
 ∵在△ACD与△ECD中,
∵在△ACD与△ECD中,
,
∴△ACD≌△ECD(ASA),
∴CA=CE;
(2)解:∵OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB,∠OAB=60°.
∵在△CDE与△ABE中,
,
∴△CDE∽△ABE,
∴DE:BE=CE:AE,
∴DE•AE=BE•CE,
∵△ACD≌△ECD,
∴AD=DE=
AE,
∵CE=CA=2OA=2AB,
∴
AE•AE=BE•2AB,
∴AE2=4BE•AB.
设AB=x,BE=y,则4xy=AE2=24(2-
),
即2xy=12(2-
) ①.
在△ABE中,∵∠ABE=90°,
∴AB2+BE2=AE2,
∴x2+y2=24(2-
) ②,
①+②,得x2+y2+2xy=36(2-
),
∵x>0,y>0,
∴x+y=3
-3
③,
②-①,得x2+y2-2xy=12(2-
),
∵x>y,
∴x-y=3
-
④,
③与④联立,解得
,
∴OA=AB=
,
∴半圆O的面积
π×(
)2=3π.
∴∠ADC=90°.
∵D是弧AB的中点,
∴
 |
| AD |
 |
| BD |
∴∠ACD=∠BCD.
 ∵在△ACD与△ECD中,
∵在△ACD与△ECD中,
|
∴△ACD≌△ECD(ASA),
∴CA=CE;
(2)解:∵OA=OB,∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=OB,∠OAB=60°.
∵在△CDE与△ABE中,
|
∴△CDE∽△ABE,
∴DE:BE=CE:AE,
∴DE•AE=BE•CE,
∵△ACD≌△ECD,
∴AD=DE=
| 1 |
| 2 |
∵CE=CA=2OA=2AB,
∴
| 1 |
| 2 |
∴AE2=4BE•AB.
设AB=x,BE=y,则4xy=AE2=24(2-
| 3 |
即2xy=12(2-
| 3 |
在△ABE中,∵∠ABE=90°,
∴AB2+BE2=AE2,
∴x2+y2=24(2-
| 3 |
①+②,得x2+y2+2xy=36(2-
| 3 |
∵x>0,y>0,
∴x+y=3
| 6 |
| 2 |
②-①,得x2+y2-2xy=12(2-
| 3 |
∵x>y,
∴x-y=3
| 2 |
| 6 |
③与④联立,解得
|
∴OA=AB=
| 6 |
∴半圆O的面积
| 1 |
| 2 |
| 6 |
点评:本题考查了圆周角定理,全等三角形、等边三角形、相似三角形的判定与性质,勾股定理,圆的面积及方程思想,综合性较强,有一定难度.

练习册系列答案
相关题目
函数y=2x-1的图象过点( )
| A、(0,1) |
| B、(-2,-3) |
| C、(1,1) |
| D、(2,-3) |
如果方程组
的解是3x+my=33的一个解,则m的值为( )
|
| A、1 | B、2 | C、3 | D、4 |
 在正方形ABCD中,N是DC的中点,M是AD上异于D的点,且∠NMB=∠MBC,则tan∠ABM的值为( )
在正方形ABCD中,N是DC的中点,M是AD上异于D的点,且∠NMB=∠MBC,则tan∠ABM的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
关于x的一元二次方程x2+2ax+(a2+1)=0的根的情况说法正确的是( )
| A、有两个实数根 |
| B、有两个不相等的实数根 |
| C、没有实数根 |
| D、无法确定 |
 如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC于点A,若BC=6cm,则BD=
如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC于点A,若BC=6cm,则BD= 如图,E是正方形ABCD边CD的中点,AE与BD交于点O,则tan∠AOB=
如图,E是正方形ABCD边CD的中点,AE与BD交于点O,则tan∠AOB=