题目内容
3.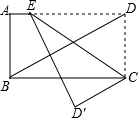 如图,将一张矩形纸片ABCD沿CE折叠,使D点落在D′点处,若CD′∥DB,∠ABD=66°,则∠DCE的度数为57°.
如图,将一张矩形纸片ABCD沿CE折叠,使D点落在D′点处,若CD′∥DB,∠ABD=66°,则∠DCE的度数为57°.
分析 根据平行线的性质由AB∥CD得∠BDC=∠ABD=66°,再利用CD′∥DB可计算出∠D′CD=114°,然后根据折叠的性质可得∠DCE=$\frac{1}{2}$∠D′CD=57°.
解答 解:∵四边形ABCD为矩形,
∴AB∥CD,
∴∠BDC=∠ABD=66°,
∵CD′∥DB,
∴∠BDC+∠D′CD=180°,
∴∠D′CD=180°-66°=114°,
∵矩形纸片ABCD沿CE折叠,使D点落在D′点处,
∴∠DCE=∠D′CE,
∴∠DCE=$\frac{1}{2}$∠D′CD=57°.
故答案为57°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质.

练习册系列答案
相关题目
 如图,若a∥b,∠1=48°,则∠2=48度.
如图,若a∥b,∠1=48°,则∠2=48度.