题目内容
19.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( )| A. | 5条 | B. | 6条 | C. | 7条 | D. | 8条 |
分析 多边形的内角和可以表示成(n-2)•180°,外角和都等于360°,故可列方程求解.
解答 解:设所求多边形边数为n,
则(n-2)•180°=3×360°-180°,
解得n=7.
故选:C.
点评 本题考查了多边形内角与外角,关键是根据多边形的内角和和外角和计算公式求多边形的边数,解答时要会根据公式进行正确运算、变形和数据处理.

练习册系列答案
相关题目
9.过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是( )
| A. | 对角线相等的四边形 | B. | 对角线垂直的四边形 | ||
| C. | 对角线互相平分且相等的四边形 | D. | 对角线互相垂直平分的四边形 |
9.已知不等式2x-a≤0的正整数解恰好是1,2,3,4,5,那么a的取值范围是( )
| A. | a>10 | B. | 10≤a≤12 | C. | 10<a≤12 | D. | 10≤a<12 |
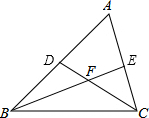 如图,在△ABC中,D是AB上一点,E是AC上一点,BE、CD相交于点F,∠A=70°,∠ACD=30°,∠ABE=25°.求:
如图,在△ABC中,D是AB上一点,E是AC上一点,BE、CD相交于点F,∠A=70°,∠ACD=30°,∠ABE=25°.求: 直线y=kx+3与y=-x+3的图象如图所示,则方程组$\left\{{\begin{array}{l}{y=kx+3}\\{y=-x+3}\end{array}}\right.$的解为$\left\{{\begin{array}{l}{x=0}\\{y=3}\end{array}}\right.$.
直线y=kx+3与y=-x+3的图象如图所示,则方程组$\left\{{\begin{array}{l}{y=kx+3}\\{y=-x+3}\end{array}}\right.$的解为$\left\{{\begin{array}{l}{x=0}\\{y=3}\end{array}}\right.$.