题目内容
9.已知不等式2x-a≤0的正整数解恰好是1,2,3,4,5,那么a的取值范围是( )| A. | a>10 | B. | 10≤a≤12 | C. | 10<a≤12 | D. | 10≤a<12 |
分析 先求出不等式的解集,再根据正整数解恰好是1,2,3,4,5,逆推a的取值范围.
解答 解:解不等式2x-a≤0得:x≤$\frac{1}{2}$a.
根据题意得:5≤$\frac{1}{2}$a<6,
解得:10≤a<12.
故选D.
点评 本题考查了一元一次不等式的整数解,解答此题要先求出不等式的解集,再根据整数解的情况确定a的取值范围.本题要求熟练掌握不等式及不等式的解法,准确的理解整数解在不等式解集中的意义,并会逆推式子中有关字母的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( )
| A. | 5条 | B. | 6条 | C. | 7条 | D. | 8条 |
19.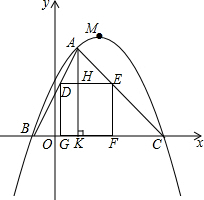 如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
(1)求出这条抛物线的解析式;
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
 如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:
如图,在平面直角坐标系xOy中,以M为顶点的抛物线与x轴分别相交于B,C两点,抛物线上一点A的横坐标为2,连接AB,AC,正方形DEFG的一边GF在线段BC上,点D,E在线段AB,AC上,AK⊥x轴于点K,交DE于点H,下表给出了这条抛物线上部分点(x,y)的坐标值:| x | … | -2 | 0 | 4 | 8 | 10 | … |
| y | … | 0 | 5 | 9 | 5 | 0 | … |
(2)求正方形DEFG的边长;
(3)请问在抛物线的对称轴上是否存在点P,在x轴上是否存在点Q,使得四边形ADQP的周长最小?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.