题目内容
9.过四边形的各个顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是( )| A. | 对角线相等的四边形 | B. | 对角线垂直的四边形 | ||
| C. | 对角线互相平分且相等的四边形 | D. | 对角线互相垂直平分的四边形 |
分析 由矩形的性质得出∠E=90°,由平行线的性质得出∠EAO=∠EBO=90°,证出四边形AEBO是矩形,得出∠AOB=90°即可.
解答 解:如图所示: ∵四边形EFGH是矩形,
∵四边形EFGH是矩形,
∴∠E=90°,
∵EF∥AC,EH∥BD,
∴∠E+∠EAG=180°,∠E+∠EBO=180°,
∴∠EAO=∠EBO=90°,
∴四边形AEBO是矩形,
∴∠AOB=90°,
∴AC⊥BD,
故选:B.
点评 本题考查了矩形的性质与判定、平行线的性质;熟练掌握矩形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.正比例函数y=-2x的图象经过的点是( )
| A. | (1,2) | B. | (1,-2) | C. | (-2,1) | D. | (-2,-1) |
17.若(x-1)2-9=0,则x=( )
| A. | ±9 | B. | ±3 | C. | 4或-2 | D. | -4或2 |
1.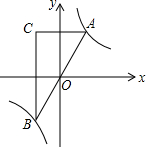 如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
 如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )
如图,已知点A是双曲线y=$\frac{2}{x}$在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为( )| A. | n=-2m | B. | n=-$\frac{2}{m}$ | C. | n=-4m | D. | n=-$\frac{4}{m}$ |
19.一个多边形的内角和比它的外角和的3倍少180°,这个多边形的边数是( )
| A. | 5条 | B. | 6条 | C. | 7条 | D. | 8条 |
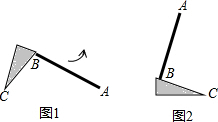 如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为105°.
如图1,教室里有一只倒地的装垃圾的灰斗,BC与地面的夹角为50°,∠C=25°,小贤同学将它扶起平放在地面上(如图2),则灰斗柄AB绕点C转动的角度为105°.
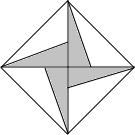 如图,正方形的阴影部分是由四个直角边长都是1和3的直角三角形组成的,假设可以在正方形内部随意取点,那么这个点取在阴影部分的概率为$\frac{1}{3}$.
如图,正方形的阴影部分是由四个直角边长都是1和3的直角三角形组成的,假设可以在正方形内部随意取点,那么这个点取在阴影部分的概率为$\frac{1}{3}$.