题目内容
14.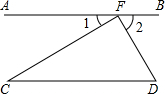 如图,CF⊥DF,且∠1与∠D互余.
如图,CF⊥DF,且∠1与∠D互余.(1)试判断AB,CD的位置关系;
(2)如条件改为AB∥CD,∠1与∠D互余,你能判断CF和DF的位置关系吗?并说明理由.
分析 (1)根据互余的性质以及等量代换证明∠D=∠2,然后利用平行线的判定定理即可证明;
(2)利用平行线的性质定理证明∠D=∠2,然后证明∠1+∠2=90°,据此即可证得.
解答 解:(1)∵CF⊥DF,
∴∠CFD=90°,
∴∠1+∠2=90°,
又∵∠1和∠D互余,
∴∠D=∠2,
∴AB∥CD;
(2)∵AB∥CD,
∴∠D=∠2,
又∵∠1和∠D互余,
∴∠1和∠2互余,即∠1+∠2=90°,
∴∠CFD=90°,
∴CF⊥DF.
点评 本题考查了平行线的判定与性质,解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
5.抛物线y=a(x-1)(x+3)(a≠0)的对称轴是直线( )
| A. | 直线x=1 | B. | 直线x=-1 | C. | 直线x=-3 | D. | 直线x=3 |
2.若x轴上的点P到y轴的距离为1,则点P的坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (1,0)或(-1,0) | D. | (0,1)或(0,-1) |
6.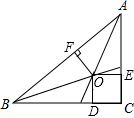 如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别为( )
如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别为( )
 如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别为( )
如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到三边AB、AC和BC的距离分别为( )| A. | 2cm、2cm、2cm | B. | 3cm、3cm、3cm | C. | 4cm、4cm、4cm | D. | 2cm、3cm、5cm |
 如图,△ABC经过一定的变换得到△A1B1C1,若△ABC上一点M的坐标为(m,n),那么M的对应点M1的坐标为(m+4,n+2).
如图,△ABC经过一定的变换得到△A1B1C1,若△ABC上一点M的坐标为(m,n),那么M的对应点M1的坐标为(m+4,n+2). 在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.
在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.