题目内容
5.抛物线y=a(x-1)(x+3)(a≠0)的对称轴是直线( )| A. | 直线x=1 | B. | 直线x=-1 | C. | 直线x=-3 | D. | 直线x=3 |
分析 首先求得抛物线与x轴的两个交点坐标,利用二次函数的对称性求得对称轴即可.
解答 解:∵抛物线y=a(x-1)(x+3)(a≠0),
∴与x轴的两个交点坐标为(1,0),(-3,0),
∴对称轴是直线x=$\frac{1-3}{2}$=-1.
故选:B.
点评 此题考查二次函数的性质,掌握抛物线的交点式求得与x轴的交点是解决问题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
13.某工厂计划生产500台电视机,实际增产$\frac{1}{5}$,实际生产电视机( )
| A. | 520台 | B. | 550台 | C. | 600台 | D. | 620台 |
 已知:如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E.若要证明BD=CE,则只要证明△BDC≌△CEB.
已知:如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D、E.若要证明BD=CE,则只要证明△BDC≌△CEB.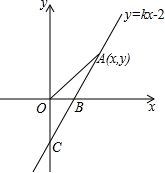 如图,直线y=kx-2与x轴、y轴分别交于B、C两点,OB:OC=$\frac{1}{2}$.
如图,直线y=kx-2与x轴、y轴分别交于B、C两点,OB:OC=$\frac{1}{2}$. 如图,△DEF是由△ABC绕某点旋转得到,请画出这两个图形的对称中心(不写作法).
如图,△DEF是由△ABC绕某点旋转得到,请画出这两个图形的对称中心(不写作法).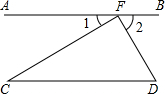 如图,CF⊥DF,且∠1与∠D互余.
如图,CF⊥DF,且∠1与∠D互余.