题目内容
2.如图1,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE内点A′的位置,探索∠A与∠1+∠2之间的数量关系,并说明理由(1)如图2,将△ABC中纸片沿DE折叠,使点A落在四边形DBCE的外部点A′的位置,探索∠A与∠1、∠2之间的数量关系,并说明理由;
(2)如图3,将四边形ABCD沿EF折叠,使点A、D落在四边形BCFE内部点A′D′的位置,请直接写出∠A、∠D、∠1与∠2之间的数量关系.

分析 根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°-∠A,代入∠1+∠2=180°+180°-2(∠AED+∠ADE)求出即可;
(1)运用三角形的外角性质即可解决问题;
(2)先根据翻折的性质表示出∠3、∠4,再根据四边形的内角和定理列式整理即可得解.
解答 解:图1中,2∠A=∠1+∠2,
理由是:∵沿DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°-∠A,∠1+∠2=180°+180°-2(∠AED+∠ADE),
∴∠1+∠2=360°-2(180°-∠A)=2∠A;
(1)如图2,2∠A=∠1-∠2.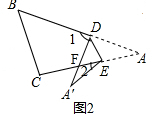
∵∠1=∠DFA+∠A,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2=2∠A+∠2,
∴2∠A=∠1-∠2;
(2)如图3,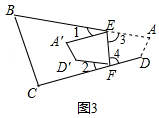
根据翻折的性质,∠3=$\frac{1}{2}$(180-∠1),∠4=$\frac{1}{2}$(180-∠2),
∵∠A+∠D+∠3+∠4=360°,
∴∠A+∠D+$\frac{1}{2}$(180-∠1)+$\frac{1}{2}$(180-∠2)=360°,
整理得,2(∠A+∠D)=∠1+∠2+360°.
点评 本题考查了折叠的性质,三角形外角性质,三角形内角和定理及四边形内角和的应用,主要考查学生运用定理进行推理和计算的能力.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
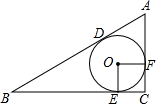 如图,⊙O是△ABC的内切圆,切点为D,E,F,∠C=90°,
如图,⊙O是△ABC的内切圆,切点为D,E,F,∠C=90°, 如图所示,等边三角形ABC的边长为6cm,它的高AD与边AB的比是多少?
如图所示,等边三角形ABC的边长为6cm,它的高AD与边AB的比是多少?
 (1)如图,在△ABC中,∠A=60°,BD,CD分别平分∠ABC和∠ACB,求∠BDC的度数.
(1)如图,在△ABC中,∠A=60°,BD,CD分别平分∠ABC和∠ACB,求∠BDC的度数.