题目内容
1.解方程(1)x2-6x+5=0 (配方法)
(2)x2-x-12=0.
(3)x2+x-3=0(公式法)
(3)x(x-3)=x-3.
分析 (1)利用配方法得到(x-3)2=4,然后利用直接开平方法解方程;
(2)利用因式分解法解方程;
(3)先计算出判别式的值,然后利用求根公式法解方程;
(4)先移项得到x(x-3)-(x-3)=0,然后利用因式分解法解方程.
解答 解:(1)x2-6x+9=4,
(x-3)2=4,
x-3=±2,
所以x1=5,x2=1;
(2)(x-4)(x+3)=0,
x-4=0或x+3=0,
所以x1=4,x2=-3;
(3)△=12-4×1×(-3)=13,
x=$\frac{-1±\sqrt{13}}{2}$,
所以x1=$\frac{-1+\sqrt{13}}{2}$,x2=$\frac{-1-\sqrt{13}}{2}$;
(4)x(x-3)-(x-3)=0,
(x-3)(x-1)=0,
x-3=0或x-1=0,
所以x1=3,x2=1.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法和公式法解一元二次方程.

练习册系列答案
相关题目
6.某自行车厂计划每天生产200辆自行车,但由于种种原因,实际每天生产量与计划量相比有出入.表是某周的生产情况(超产记为正、减产记为负):
(1)根据记录的数据可知该厂星期四生产自行车212辆;
(2)产量最多的一天比产量最少的一天多生产自行车26辆;
(4)该厂实行每周计件工资制,每生产一辆车可得30元,若超额完成任务,则超过部分每辆另奖20元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -2 | -4 | +12 | -10 | +16 | -8 |
(2)产量最多的一天比产量最少的一天多生产自行车26辆;
(4)该厂实行每周计件工资制,每生产一辆车可得30元,若超额完成任务,则超过部分每辆另奖20元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少元?
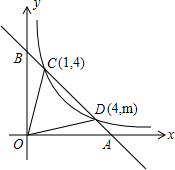 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第一象限C,D两点,坐标轴交于A、B两点,连结OC,OD(O是坐标原点). 如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,AB=5,则cos∠BCD的值为$\frac{4}{5}$.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若AC=4,AB=5,则cos∠BCD的值为$\frac{4}{5}$. 如图,在平面直角坐标系中,已知正方形OABC的顶点坐标分别为O(0,0),A(3,0),B(3,3),C(0,3).
如图,在平面直角坐标系中,已知正方形OABC的顶点坐标分别为O(0,0),A(3,0),B(3,3),C(0,3).