题目内容
 在△ABC中,已知AB=37,AC=58,在BC上有一点D使得AB=AD,且D在B、C之间.若BD与DC的长度都是整数,则BD的长度是
在△ABC中,已知AB=37,AC=58,在BC上有一点D使得AB=AD,且D在B、C之间.若BD与DC的长度都是整数,则BD的长度是考点:三角形边角关系
专题:
分析:首先过点A作AH⊥BC于H,由勾股定理可得:AC2=AH2+CH2,AB2=AH2+BH2,则可得AC2-AB2=CH2-BH2=(CH+BH)(CH-BH)=BC×CD.由AB=37,AC=58,可得BC×CD=3×5×7×19,然后根据三角形三边关系与BD与DC的长度都是整数,确定BC=35或57,然后分析求解即可求得答案.
解答: 解:过点A作AH⊥BC于H,
解:过点A作AH⊥BC于H,
则AC2=AH2+CH2,AB2=AH2+BH2,
故AC2-AB2=CH2-BH2=(CH+BH)(CH-BH)=BC×CD.
∵AB=37,AC=58,
∴BC×CD=582-372=3×5×7×19.
∵AC-AB<BC<AC+AB,
∴21<BC<95,
∵BC为整数,
∴BC=35或BC=57.
若BC=35,则CD=3×19=57>BC,D不在B、C之间,故应舍去.
∴应取BC=57,这时CD=35,BD=22.
故答案为:22.
 解:过点A作AH⊥BC于H,
解:过点A作AH⊥BC于H,则AC2=AH2+CH2,AB2=AH2+BH2,
故AC2-AB2=CH2-BH2=(CH+BH)(CH-BH)=BC×CD.
∵AB=37,AC=58,
∴BC×CD=582-372=3×5×7×19.
∵AC-AB<BC<AC+AB,
∴21<BC<95,
∵BC为整数,
∴BC=35或BC=57.
若BC=35,则CD=3×19=57>BC,D不在B、C之间,故应舍去.
∴应取BC=57,这时CD=35,BD=22.
故答案为:22.
点评:此题考查了三角形的三边关系、勾股定理以及平方差公式等知识.此题难度较大,解题的关键是准确作出辅助线,注意数形结合与分类讨论思想的应用.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知|a|>a,|b|>b,且|a|>|b|,则a、b的大小关系为( )
| A、a>b | B、a=b |
| C、a<b | D、无法确定 |
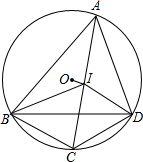 如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:
如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证: 如图,半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2,且MN在正方形的对角线BD上,则正方形的边长为
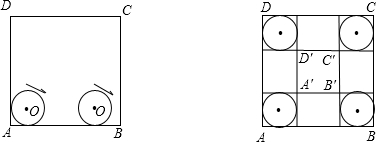
如图,半径为2的⊙O与正方形ABCD相切于点P、Q,弦MN=2,且MN在正方形的对角线BD上,则正方形的边长为


