题目内容
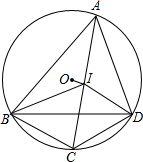 如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:
如图,⊙O的内接四边形ABCD中,AC,BD是它的对角线,AC的中点I是△ABD的内心.求证:(1)OI是△IBD的外接圆的切线;
(2)AB+AD=2BD.
考点:三角形的内切圆与内心,全等三角形的判定与性质,切线的判定
专题:证明题
分析:(1)根据三角形内心的性质和同弧上圆周角的性质,以及等角对等边即可证得C是△IBD的外心,然后证得OI⊥CI,即可证得OI是△IBD的外接圆的切线;
(2)根据(1)可以得到AI=CD,AB=2BF,即可证得.
(2)根据(1)可以得到AI=CD,AB=2BF,即可证得.
解答: 解:(1)∵∠CID=∠IAD+∠IDA,∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA
解:(1)∵∠CID=∠IAD+∠IDA,∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA
∴∠CID=∠CDI,
∴CI=CD.
同理,CI=CB.
故点C是△IBD的外心.
连接OA,OC,
∵I是AC的中点,且OA=OC,
∴OI⊥AC,即OI⊥CI.
∴OI是△IBD外接圆的切线.
(2)由(1)可得:
∵AC的中点I是△ABD的内心,
∴∠BAC=∠CAD
∴∠BDC=∠DAC=∠BAC,
又∵∠ACD=∠DCF,
∴△ADC∽△DFC,
∴
=
,
∵AC=2CI
∴AC=2CD
∴AD=2DF
同理可得:AB=2BF
∴AB+AD=2BF+2DF=2BD.
 解:(1)∵∠CID=∠IAD+∠IDA,∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA
解:(1)∵∠CID=∠IAD+∠IDA,∠CDI=∠CDB+∠BDI=∠BAC+∠IDA=∠IAD+∠IDA∴∠CID=∠CDI,
∴CI=CD.
同理,CI=CB.
故点C是△IBD的外心.
连接OA,OC,
∵I是AC的中点,且OA=OC,
∴OI⊥AC,即OI⊥CI.
∴OI是△IBD外接圆的切线.
(2)由(1)可得:
∵AC的中点I是△ABD的内心,
∴∠BAC=∠CAD
∴∠BDC=∠DAC=∠BAC,
又∵∠ACD=∠DCF,
∴△ADC∽△DFC,
∴
| AC |
| CD |
| AD |
| DF |
∵AC=2CI
∴AC=2CD
∴AD=2DF
同理可得:AB=2BF
∴AB+AD=2BF+2DF=2BD.
点评:本题考查了圆的切线的证明,以及三角形的内心的计算,证得C是△IBD的外心是关键.

练习册系列答案
相关题目
某校初三•一班学生参加体育加试,第一小组引体向上的成绩如下表所示:
则这组学生引体向上个数的众数和中位数分别为( )
| 引体向上的个数 | 7 | 8 | 9 | 10 |
| 人数 | 2 | 1 | 4 | 5 |
| A、9.5和10 |
| B、9和10 |
| C、10和9.5 |
| D、10和9 |
 已知,一次函数y=x+m-2与二次函数y=x2-2的图象从左至右的交点依次为点B、A.
已知,一次函数y=x+m-2与二次函数y=x2-2的图象从左至右的交点依次为点B、A.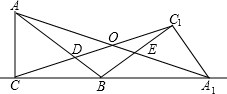 (S△AOD+S△A1BE)-(S△C1OE+S△CBD)=
(S△AOD+S△A1BE)-(S△C1OE+S△CBD)= 在△ABC中,已知AB=37,AC=58,在BC上有一点D使得AB=AD,且D在B、C之间.若BD与DC的长度都是整数,则BD的长度是
在△ABC中,已知AB=37,AC=58,在BC上有一点D使得AB=AD,且D在B、C之间.若BD与DC的长度都是整数,则BD的长度是