题目内容
 某工厂生产的边长为l米的正方形装饰材料ABCD如图所示,点E在BC上,点F是CD的中点,△ABE、△CEF和四边形AEFD分别由Ⅰ型、Ⅱ型、Ⅲ型三种材料制成.
某工厂生产的边长为l米的正方形装饰材料ABCD如图所示,点E在BC上,点F是CD的中点,△ABE、△CEF和四边形AEFD分别由Ⅰ型、Ⅱ型、Ⅲ型三种材料制成.(1)设BE=x,请用含x的代数式分别表示△ABE和△EFC的面积;
(2)己知1型、Ⅱ型、Ⅲ型三种材料每平方米的价格分别为50元、100元和40元,若要求制成这样一块装饰材料的成本为50元,求点E的位置;
(3)由于市场变化,1型材科和Ⅱ型材料每平方米的价格变为70元和80元,Ⅲ型材料的价格不变,现仍要生产(2)中式样的装饰材料,则每块的成本将有何变化?变化多少元?
考点:列代数式,代数式求值
专题:
分析:(1)根据三角形的面积公式列式整理即可得解;
(2)用单价乘以面积,然后把三部分价格相加等于成本50元,列出方程求解即可;
(3)把各部分的单价乘以相应的面积,列式计算即可得解.
(2)用单价乘以面积,然后把三部分价格相加等于成本50元,列出方程求解即可;
(3)把各部分的单价乘以相应的面积,列式计算即可得解.
解答:解:(1)S△ABE=
AB•BE=
×1×x=
x,
S△EFC=
EC•FC=
×(1-x)×
=
(1-x);
(2)Ⅲ型材料的面积为12-
x-
(1-x)=
-
x,
所以,50×
x+100×
(1-x)+40×(
-
x)=50,
解得x=
,
∴点E在BC的中点处;
(3)70×
×
+80×
(1-
)+40×(
-
×
)
=17.5+10+25
=52.5元.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
S△EFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)Ⅲ型材料的面积为12-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
所以,50×
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
解得x=
| 1 |
| 2 |
∴点E在BC的中点处;
(3)70×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
=17.5+10+25
=52.5元.
点评:本题考查了列代数式,主要利用了直角三角形的面积公式,难点在于表示出材料Ⅲ所占的面积.

练习册系列答案
相关题目
如果方程2x+8=-6与关于x的方程2x-3a=-5的解相同,则a的值为( )
| A、13 | B、3 | C、-3 | D、8 |

 如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,求AD的长.
如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,求AD的长.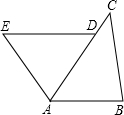 (1)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动,第一天收到捐款10000元,第三天收到捐款12100元,如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
(1)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动,第一天收到捐款10000元,第三天收到捐款12100元,如果第二天、第三天收到捐款的增长率相同,求捐款增长率? 超速行驶是引发交通事故的主要原因.某校数学课外小组的几个同学想用自己所学的知识检测车速,如图,他们将观测点设在到公路l的距离为0.1千米的P处,这时,一辆轿车由西向东匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°.如果这段高速公路的限速是每小时90千米(即最高时速不超过90千米),试判断此车是否超速?
超速行驶是引发交通事故的主要原因.某校数学课外小组的几个同学想用自己所学的知识检测车速,如图,他们将观测点设在到公路l的距离为0.1千米的P处,这时,一辆轿车由西向东匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°.如果这段高速公路的限速是每小时90千米(即最高时速不超过90千米),试判断此车是否超速?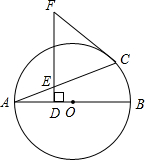 如图,AB是⊙O的直径,DF⊥AB于点D,交弦AC于点E,FC=FE.
如图,AB是⊙O的直径,DF⊥AB于点D,交弦AC于点E,FC=FE. 如图,点E、F在AB上,且AF=BE,AC=BD,AC∥BD.求证:CF∥DE.
如图,点E、F在AB上,且AF=BE,AC=BD,AC∥BD.求证:CF∥DE.