题目内容
15.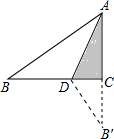 如图,在△ABC中,AB=20,AC=12,BC=16,把△ABC折迭,使AB落在直线AC上,则重迭部分(阴影部分)的面积是36.
如图,在△ABC中,AB=20,AC=12,BC=16,把△ABC折迭,使AB落在直线AC上,则重迭部分(阴影部分)的面积是36.
分析 利用勾股定理求出CD=6,所以阴影部分面积为$\frac{1}{2}$×CD×AC,求出即可.
解答 解:设CD=x,
∵在△ABC中,AB=20,AC=12,BC=16,把△ABC折叠,使AB落在直线AC上,
∴BD=B′D=16-x,B′C=AB-AC=20-12=8,∠DCB′=90°,
∴在Rt△DCB′中,
CD2+B′C2=DB′2,
∴x2+82=(16-x)2,
解得:x=6,
∴重叠部分(阴影部分)的面积为:$\frac{1}{2}$×6×12=36.
故答案为:36.
点评 此题主要考查了翻折变换的性质以及勾股定理等知识,根据已知得出BD=B′D=16-x,B′C=8是解题关键.

练习册系列答案
相关题目
4.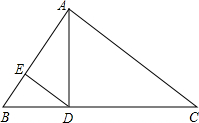 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,若AD=3,DE=2,则AC=( )
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,若AD=3,DE=2,则AC=( )
 如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,若AD=3,DE=2,则AC=( )
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,若AD=3,DE=2,则AC=( )| A. | $\frac{21}{2}$ | B. | $\frac{\sqrt{15}}{2}$ | C. | $\frac{9}{2}$ | D. | $\sqrt{15}$ |
5.随着经济的发展,节能与环保问题越来越得到重视,据宁波环境保护局披露:2015年宁波市区节能环保支出将达到18957.74万元.18957.74万元用科学记数法应记为( )
| A. | 18957.74×104元 | B. | 1.895774×107元 | C. | 1.895774×108元 | D. | 1.895774×109元 |
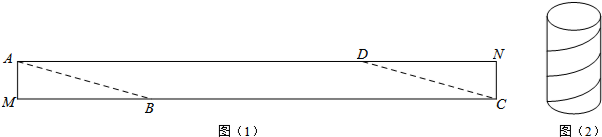
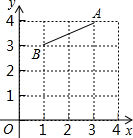 如图,在平面直角坐标系中,将线段AB绕点B按顺时针方向旋转90°后,得到线段A′B,则点A′的坐标为(2,1).
如图,在平面直角坐标系中,将线段AB绕点B按顺时针方向旋转90°后,得到线段A′B,则点A′的坐标为(2,1).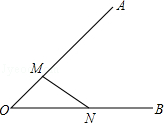 如图,在图中求作一⊙P,使⊙P满足是以线段MN为弦且圆心P到∠AOB两边的距离相等,保留作图痕迹不写出作法.(要求:用尺规作图)
如图,在图中求作一⊙P,使⊙P满足是以线段MN为弦且圆心P到∠AOB两边的距离相等,保留作图痕迹不写出作法.(要求:用尺规作图)