题目内容
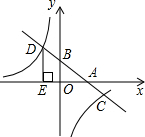 如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y=
如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y=| m |
| x |
(1)求m的值;
(2)写出反比例函数的表达式,并求出D点的坐标;
(3)根据图象直接回答:当x为何值时,一次函数的值大于反比例函数的值?
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)根据反比例函数与一次函数的交点问题,把C点坐标代入y=
即可求得m的值;
(2)由(1)得反比例函数的解析式为y=-
,由DE=3得到D的纵坐标,然后把y=3代入反比例函数解析式计算出对应的自变量的值,从而确定D点坐标;
(3)观察函数图象得到当x<-2或0<x<6时,一次函数图象都在反比例函数图象上方.
| m |
| x |
(2)由(1)得反比例函数的解析式为y=-
| 6 |
| x |
(3)观察函数图象得到当x<-2或0<x<6时,一次函数图象都在反比例函数图象上方.
解答:解:(1)把C(6,-1)代入y=
得m=6×(-1)=-6;
(2)反比例函数的解析式为y=-
,
把y=3代入y=-
得x=-2,
∴D点坐标为(-2,3);
(2)当x<-2或0<x<6时.一次函数的值大于反比例函数的值.
| m |
| x |
(2)反比例函数的解析式为y=-
| 6 |
| x |
把y=3代入y=-
| 6 |
| x |
∴D点坐标为(-2,3);
(2)当x<-2或0<x<6时.一次函数的值大于反比例函数的值.
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了观察函数图象的能力.

练习册系列答案
相关题目
 如图,AB=DB,BC=BE,∠1=∠2,问∠A与∠D相等吗?为什么?
如图,AB=DB,BC=BE,∠1=∠2,问∠A与∠D相等吗?为什么? 如图,CD为△ABC的角平分线,∠DCB=30°,BC=AC+AD,求∠A的度数.
如图,CD为△ABC的角平分线,∠DCB=30°,BC=AC+AD,求∠A的度数.