题目内容
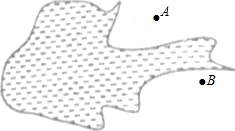如图所示，某湖泊岸有A、B两棵大树，想在两棵大树间架一条电话线路．为了计算两棵大树能承受的压力，需测量出A、B之间的距离，但是A、B两点又不能直接到达，你能用已学过的知识和方法设计测量方案，求出A、B两点间的距离吗？并说明理由．考点：全等三角形的应用
专题：
分析：首先找一点C，连接AC，BC，并延长，截取CD=BC，AC=EC，可证△EDC≌△ABC，即可证明DE=BA．
解答：
解：能求出A、B两点间的距离，
理由：找一点C，连接AC，BC，并延长，截取使CD=BC，AC=EC，
在△EDC和△ABC中，
，
∴△EDC≌△ABC（SAS），
∴AB=ED，
即量出ED的长即可得出答案．
解：能求出A、B两点间的距离，理由：找一点C，连接AC，BC，并延长，截取使CD=BC，AC=EC，
在△EDC和△ABC中，
|
∴△EDC≌△ABC（SAS），
∴AB=ED，
即量出ED的长即可得出答案．
点评：本题考查了全等三角形在实际生活中的应用，全等三角形的证明，全等三角形对应边相等的性质，本题中求证△EDC≌△ABC是解题的关键．
练习册系列答案
相关题目
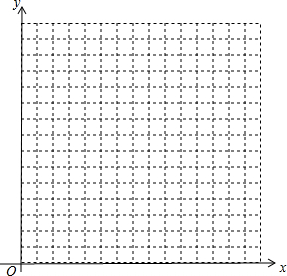在下面的直角坐标系中描出下列各点，顺次用线段将下面各点连起来，并将最后一点与第一点连接起来，看看得到的是一个什么图形？（2，2），（5，2），（7，0），（9，2），（12，2），（12，5）（14，7），（12，9），（12，12），（9，12），（7，14），（5，12），（2，12），（2，9），（0，7），（2，5）甲上午6时步行从A地出发于下午5时到达B地，乙上午10时骑自行车从A地出发于下午3时到达B地，则乙追上甲的时间为（ ）
| A、12时20分 |
| B、13时20分 |
| C、14时20分 |
| D、11时20分 |
如图，菱形ABCD中，AB=4，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为
在四边形ABCD中，AB=2，BC=
如图是由大小相同的小正方体组成的简单几何体的主视图和左视图，那么组成这个几何体的小正方体的个数最少为