题目内容
10.下列各数中无理数是( )| A. | $\sqrt{4}$ | B. | 3.14 | C. | -π | D. | $\frac{22}{7}$ |
分析 无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解答 解:A、$\sqrt{4}$=2是整数,是有理数,故选项不符合题意;
B、3.14是有限小数,是有理数,故选项不符合题意;
C、-π是无理数,选项符合题意;
D、$\frac{22}{7}$是分数,是有理数,选项不符合题意.
故选C.
点评 此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
相关题目
20.一个角的两边分别平行于另一个角的两边,则这两个角( )
| A. | 相等 | B. | 相等或互补 | C. | 互补 | D. | 不能确定 |
1.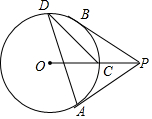 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )
 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )| A. | 26° | B. | 20° | C. | 16° | D. | 30° |
18.正方形具有而矩形不具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线相等 | ||
| C. | 对角线互相平分且相等 | D. | 对角线互相垂直 |
15.下列命题为真命题的是( )
| A. | 由两边及一角对应相等的两三角形全等 | |
| B. | 两个相似三角形的面积比等于其相似比 | |
| C. | 同旁内角相等 | |
| D. | 两组对边分别相等的四边形是平行四边形 |
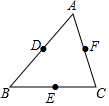 如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中能画平行四边形的个数是( )
如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中能画平行四边形的个数是( )