题目内容
13. 如果一条抛物线y=ax2+bx+c(a≠0)与x轴的两个交点为A,B(点A在点B的左侧),顶点为P,连接PA,PB,那么称△PAB为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴的两个交点为A,B(点A在点B的左侧),顶点为P,连接PA,PB,那么称△PAB为这条抛物线的“抛物线三角形”.(1)请写出“抛物线三角形”是等腰直角三角形时,抛物线的表达式(写出一个即可);
(2)若抛物线y=-x2+bx(b>0)的“抛物线三角形”是等边三角形,求b的值;
(3)若抛物线y=ax2+bx+c(a≠0)不存在“抛物线三角形”,则a、b、c之间应满足怎样的关系式?请直接写出.
分析 (1)利用等腰直角三角形的性质可知P点的纵坐标为AB的一半,据此可设出P、A、B的坐标,可写出抛物线的表达式;
(2)过点P作PH⊥AB于H,由等边三角形的性质可得到PH=$\sqrt{3}$AH,再用b表示出P点坐标,则可得到关于b的方程,可求得b的值;
(3)由条件可知P、A、B三点不能构成三角形,则可知A、B重合或没有A、B两点,即抛物线与x轴有一个或没有交点,则可得到a、b、c的关系.
解答 解:
(1)不妨设抛物线的对称轴为y轴,即设抛物线解析式为y=-x2+c(c>0),
则P(0,c),A(-$\sqrt{c}$,0),B($\sqrt{c}$,0),
∵△PAB为等腰直角三角形,
∴OP=OA=OB,即c=$\sqrt{c}$,解得c=1,
∴“抛物线三角形”是等腰直角三角形时,抛物线的表达式可以为y=-x2+1;
(2)如图,过点P作PH⊥AB于H,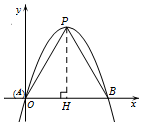
∵△PAB是等边三角形,
∴PH=$\sqrt{3}$AH,
∵抛物线y=-x2+bx(b>0)的顶点坐标为($\frac{b}{2}$,$\frac{{b}^{2}}{4}$),
∴$\frac{{b}^{2}}{4}$=$\frac{\sqrt{3}b}{2}$,解得b=2$\sqrt{3}$;
(3)当抛物线y=ax2+bx+c(a≠0)不存在“抛物线三角形”,
则P、A、B三点不能构成三角形,即抛物线与x轴有一个或没有交点,
∴方程ax2+bx+c=0(a≠0)有两个相等的实数根或没有实数根,
∴b2-4ac≤0.
点评 本题为二次函数的综合应用,涉及待定系数法、等腰直角三角形的性质、等边三角形的性质、一元二次方程与抛物线的关系等知识.在(1)(2)中利用抛物线线三角形的定义结合直角三角形得到P点纵坐标和AB的关系是解题的关键,在(3)中确定出抛物线满足的条件是解题的关键.本题考查知识点较多,综合性较强,但难度不大,关系是理解抛物线三角形的定义.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 41.5×105 | B. | 0.413×104 | C. | -12×104 | D. | -7.16×105 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
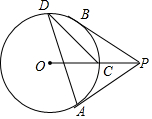 如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )
如图,过⊙O外一点P引⊙O的两条切线PA、PB,切点分别是A、B,OP交⊙O于点C,点D是优弧AB上不与点A、点B重合的一个动点,连接AD、CD,若∠APB=76°,则△ADC的度数为( )| A. | 26° | B. | 20° | C. | 16° | D. | 30° |
| A. | x2-2x-3 | B. | x2-2x+1 | C. | x2+x-3 | D. | x2-3 |
| A. | 对角线互相平分 | B. | 对角线相等 | ||
| C. | 对角线互相平分且相等 | D. | 对角线互相垂直 |
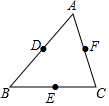 如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中能画平行四边形的个数是( )
如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中能画平行四边形的个数是( )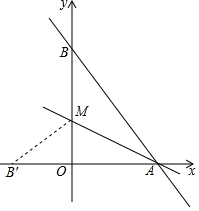 如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和点B,M是OB上的一点若将△ABM沿直线AM折叠,点B恰好落在x轴上的点B’处.
如图,直线y=-$\frac{4}{3}$x+8与x轴,y轴分别交于点A和点B,M是OB上的一点若将△ABM沿直线AM折叠,点B恰好落在x轴上的点B’处.