题目内容
10.计算与化简(1)(-$\frac{1}{2}$-$\frac{1}{3}$)÷(-$\frac{1}{6}$)+(-2)2×(-14)
(2)|-5|-(-3)2-(-$\frac{2}{3}$)3×|7-(-11)|+(-$\frac{1}{3}$)
(3)先化简,再求值
4m3-(3m2+5m-2)+2(3m+$\frac{3}{2}$m2-2m3)-1,其中m=2016.
分析 (1)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(2)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式去括号合并得到最简结果,把m的值代入计算即可求出值.
解答 解:(1)原式=5-56=-51;
(2)原式=5-9+$\frac{16}{3}$-$\frac{1}{3}$=1;
(3)原式=4m3-3m2-5m+2+6m+3m2-4m3-1=m+1,
当m=2016时,原式=2017.
点评 此题考查了整式的加减-化简求值,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.某商场试销一种商品,成本为每件100元,一段时间后,发现销售量y(件)与销售单价x(元)之间的函数关系如下表:
(1)请根据表格中所给数据,求出y关于x的函数关系式;
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
| 销售单价x(元) | … | 130 | 135 | 140 | 145 | … |
| 销售量y(件) | … | 240 | 230 | 220 | 210 | … |
(2)设商场所获利润为w元,将商品销售单价定为多少时,才能使所获利润最大?最大利润是多少?
5. 如图,南偏东15°和北偏东25°的两条射线组成的角(即∠AOB)等于( )
如图,南偏东15°和北偏东25°的两条射线组成的角(即∠AOB)等于( )
 如图,南偏东15°和北偏东25°的两条射线组成的角(即∠AOB)等于( )
如图,南偏东15°和北偏东25°的两条射线组成的角(即∠AOB)等于( )| A. | 40° | B. | 80° | C. | 140° | D. | 150° |
15.若n、n满足|2m+1|+(n-2)4=0,则mn的值等于( )
| A. | -1 | B. | $\frac{1}{4}$ | C. | -2 | D. | 1 |
20.方程3x2-8x-10=0的二次项系数和一次项系数分别为( )
| A. | 3和8 | B. | 3和-8 | C. | 3和-10 | D. | 3和10 |
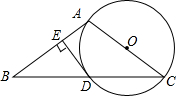 如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E. 平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).
平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(2,4),C(3,-1).