题目内容
1.(1)解方程(x-2)(x-3)=0;(2)已知关于x的一元二次方程x2-2x+m=0有两个不相等的实数根,求m的值取值范围.
分析 (1)利用因式分解法解一元二次方程,即可得出x1=2,x2=3;
(2)根据方程有两个不相等的实数根结合根的判别式即可得出关于m的一元一次不等式,解之即可得出结论.
解答 解:(1)∵(x-2)(x-3)=0
∴x-2=0或x-3=0,
解得:x1=2,x2=3.
(2)∵关于x的一元二次方程x2-2x+m=0有两个不相等的实数根,
∴△=(-2)2-4m=4-4m>0,
解得:m<1.
∴m的值取值范围为m<1.
点评 本题考查了因式分解法解一元二次方程以及根的判别式,熟练掌握“当△>0时,方程有两个不相等的两个实数根”是解题的关键.

练习册系列答案
相关题目
16.光的速度约为3000 000千米/秒,用科学记数法表示为( )
| A. | 0.3×107 | B. | 3×106 | C. | 3×105 | D. | 30×104 |
6. 如图,已知⊙O是△ABC的外接圆,若弦BC等于⊙O的半径,则∠BAC等于( )
如图,已知⊙O是△ABC的外接圆,若弦BC等于⊙O的半径,则∠BAC等于( )
 如图,已知⊙O是△ABC的外接圆,若弦BC等于⊙O的半径,则∠BAC等于( )
如图,已知⊙O是△ABC的外接圆,若弦BC等于⊙O的半径,则∠BAC等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 20° |
11.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
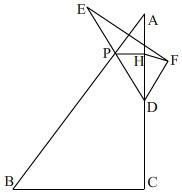 在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=$\frac{3}{5}$t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH.
在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=$\frac{3}{5}$t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH.