Question

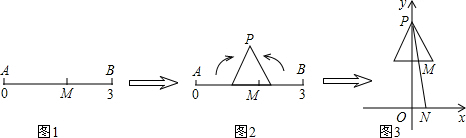
将一根绳子对折后用线段AB来表示，对折点在点B处，点P在AB上，且AP=

1

2

PB，如图所示，现从P处把绳子剪断，剪断后各段绳子中最长的一段为40cm，则这条绳子原来的长度是

 

．

Answer 1

考点：两点间的距离

专题：

分析：设AP=xcm，则BP=2xcm，分为两种情况：①当含有线段AP的绳子最长时，得出方程x+x=40，②当含有线段BP的绳子最长时，得出方程2x+2x=40，求出每个方程的解，代入2（x+2x）求出即可．

解答：解：设AP=xcm，则BP=2xcm，
①当含有线段AP的绳子最长时，x+x=40，
解得：x=20，
即绳子的原长是2（x+2x）=6x=120（cm）；
②当含有线段BP的绳子最长时，2x+2x=40，
解得：x=10，
即绳子的原长是2（x+2x）=6x=60（cm）；
故答案为：60cm或120cm．

点评：本题考查了两点间的距离的应用，解此题的关键是能根据题意求出符合条件的两个解．