题目内容
如图1,数轴上A,M,B三点对应的数分别是0,
,3;如图2,将线段AB折成正三角形,使点A,B重合于点P;如图3,建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),若PM与x轴交于点N(n,0),则n的值为 .
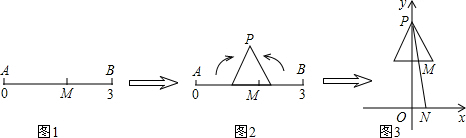
| 3 |

考点:相似三角形的判定与性质,实数与数轴,等边三角形的性质,平移的性质
专题:
分析:如图,设正三角形的底边与y轴交于点C,可求得PC=
,且由条件可证得△PCM∽△PON,利用相似比可求得ON,即可得出n的值.
| ||
| 2 |
解答: 解:如图,设正三角形的底边与y轴交于点C,
解:如图,设正三角形的底边与y轴交于点C,
∵平移,
∴MC⊥y,
∴MC∥ON
∴△PCM∽△PON,
∴
=
,
∵AB=3,
∴正三角形的边长为1,
∴PC=
,MC=
-1-
=
-
,
∵P坐标为(0,2),
∴PO=2,
∴
=
,
∴ON=4-2
,
∴n=4-2
,
故答案为:4-2
.
 解:如图,设正三角形的底边与y轴交于点C,
解:如图,设正三角形的底边与y轴交于点C,∵平移,
∴MC⊥y,
∴MC∥ON
∴△PCM∽△PON,
∴
| CM |
| ON |
| PC |
| PO |
∵AB=3,
∴正三角形的边长为1,
∴PC=
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 2 |
∵P坐标为(0,2),
∴PO=2,
∴
| ||||
| ON |
| ||||
| 2 |
∴ON=4-2
| 3 |
∴n=4-2
| 3 |
故答案为:4-2
| 3 |
点评:本题主要考查相似三角形的判定和性质,利用条件求得CM和PC的长是解题的关键,注意等边三角形性质的运用.

练习册系列答案
相关题目
与
是同类二次根式的是( )
| 3 |
A、2
| ||
B、
| ||
| C、3 | ||
D、
|
 如图所示,已知线段AB=8cm,BC=3cm,点M、N分别是线段AC、BC的中点,求线段MN的长度;若线段BC为任意长度,其他条件不变,则线段M你的长度是否发生变化?请说明理由.
如图所示,已知线段AB=8cm,BC=3cm,点M、N分别是线段AC、BC的中点,求线段MN的长度;若线段BC为任意长度,其他条件不变,则线段M你的长度是否发生变化?请说明理由. 将一根绳子对折后用线段AB来表示,对折点在点B处,点P在AB上,且AP=
将一根绳子对折后用线段AB来表示,对折点在点B处,点P在AB上,且AP=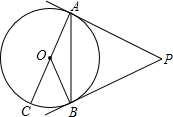 如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,求∠BAC的度数.
如图,PA,PB是⊙O是切线,A,B为切点,AC是⊙O的直径,若∠P=46°,求∠BAC的度数. 把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合,按照如图的方式叠合在一起,连接EB,交HI于点J,则∠BJI的大小为
把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合,按照如图的方式叠合在一起,连接EB,交HI于点J,则∠BJI的大小为