题目内容
5.已知:关于x的一元二次方程x2-(2m+3)x+m2+3m+2=0(m为实数)的两个实数根分别是△ABC的两边AB、AC的长,且第三边BC的长为5.当m取何值时,△ABC为直角三角形?分析 首先利用根的判别式,判定无论m取何值,方程总有两个不相等的实数根,然后利用公式法求出两个解,再设AB=m+1,AC=m+2,则AB<AC,再分情况计算:①当BC为直角边时,②当BC为斜边时,分别算出m的值.
解答 解:∵a=1,b=-(2m+3),c=m2+3m+2,
∴△=b2-4ac,
=[-(2m+3)]2-4(m2+3m+2),
=4m2+12m+9-4m2-12m-8,
=1>0,
∴无论m取何值,方程总有两个不相等的实数根,
由求根公式得:$x=\frac{{-b±\sqrt{{b^2}-4ac}}}{2a}=\frac{{({2m+3})±1}}{2}$,
即x1=m+2,x2=m+1,
不妨设AB=m+1,AC=m+2,则AB<AC,
∵△ABC为直角三角形且第三边BC=5,
当BC为直角边时,由勾股定理得:
AB2+BC2=AC 2
∴(m+1)2+52=(m+2)2,
解得m=11,
当BC为斜边时,由勾股定理得:AB2+AC2=BC2,
∴(m+1)2+(m+2)2=52,
解得m1=2,m2=-5,
当m=-5时,AB=m+1=-4,
∴m=-5(舍去)
∴m=11或m=2时,△ABC为直角三角形.
点评 此题主要考查了一元二次方程根的判别式,以及勾股定理逆定理的应用,关键是要分情况讨论,不要漏解.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
10.下列长度的三根木棒首尾相接,不能做成三角形框架的是( )
| A. | 6cm、7cm、1cm | B. | 7cm、13cm、10cm | C. | 6cm、7cm、12cm | D. | 5cm、9cm、13cm |
15.下列调查适合用普查的方法是( )
| A. | 调查一批灯泡的使用寿命 | B. | 调查太平洋里的水的酸碱度 | ||
| C. | 调查某班学生的身高 | D. | 调查全国中学生每天看电视的时间 |
 已知:一次函数y1=x+2与反比例函数y2=$\frac{k}{x}$ 相交于A、B两点且A点的纵坐标为4.
已知:一次函数y1=x+2与反比例函数y2=$\frac{k}{x}$ 相交于A、B两点且A点的纵坐标为4.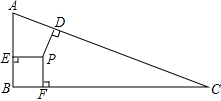 如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,PE⊥AB、PF⊥BC、PD⊥AC,垂足分别为E、F、D,求PD的长.
如图,△ABC中,∠B=90°,两直角边AB=7,BC=24,三角形内有一点P到各边的距离相等,PE⊥AB、PF⊥BC、PD⊥AC,垂足分别为E、F、D,求PD的长. 已知:如图,在平行四边形ABCD中,F是AB上一点,连结DF并延长交CB的延长线于E.求证:AD•AB=AF•CE.
已知:如图,在平行四边形ABCD中,F是AB上一点,连结DF并延长交CB的延长线于E.求证:AD•AB=AF•CE.