Question

13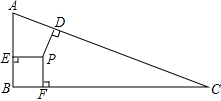．如图，△ABC中，∠B=90°，两直角边AB=7，BC=24，三角形内有一点P到各边的距离相等，PE⊥AB、PF⊥BC、PD⊥AC，垂足分别为E、F、D，求PD的长．

Answer 1

分析 连接AP，BP，CP，根据直角三角形的面积公式即可求得该距离的长．

解答 解：连接AP，BP，CP．
设PE=PF=PD=x．
∵△ABC中，∠B=90°，两直角边AB=7，BC=24，
∴AC=25．
∵S_△ABC=$\frac{1}{2}$×AB×CB=84，
S_△ABC=$\frac{1}{2}$AB×x+$\frac{1}{2}$AC×x+$\frac{1}{2}$BC×x=$\frac{1}{2}$（AB+BC+AC）•x=$\frac{1}{2}$×56x=28x，
则28x=84，
x=3．
故PD的长为3．

点评 本题考查了勾股定理，三角形的面积．注意构造辅助线，则直角三角形的面积有两种表示方法：一是整体计算，即两条直角边乘积的一半；二是等于三个小三角形的面积和，即$\frac{1}{2}$（AB+AC+BC）x，然后即可计算x的值．