题目内容
18.将正方形按如图所示方式排列,按此方式摆下去,第n幅图中共有$\frac{1}{2}$n(n+1)个正方形(用含n的代数式表示).
分析 由图形可知:第1幅图中共有1个正方形,第2幅图中共有1+2=3个正方形,第3幅图中共有1+2+3=6个正方形,…由此得出第n幅图中共有1+2+3+…+n=$\frac{1}{2}$n(n+1)个正方形.
解答 解:∵第1幅图中共有1个正方形,
第2幅图中共有1+2=3个正方形,
第3幅图中共有1+2+3=6个正方形,
…
∴第n幅图中共有1+2+3+…+n=$\frac{1}{2}$n(n+1)个正方形.
故答案为:$\frac{1}{2}$n(n+1).
点评 此题考查图形的变化规律,找出图形排列的规律,得出运算的方法,利用计算方法解决问题.

练习册系列答案
相关题目
3.已知等边三角形的高为3,则边长为( )
| A. | 1.5 | B. | 2$\sqrt{3}$ | C. | 6 | D. | $\sqrt{3}$ |
10.若最简二次根式$\sqrt{3a-8}$与$\sqrt{17-2a}$是同类二次根式,则a的取值为( )
| A. | a=4 | B. | a=5 | C. | a=6 | D. | a=7 |
8.若⊙O1与⊙O2相切,且它们的半径分别是方程x2-6x+5=0的两根,则圆心距为( )
| A. | 1 | B. | 5 | C. | 4或6 | D. | 1或5 |
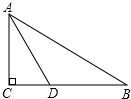 如图所示,在△ABC中,∠C=90°,D点在线段AB的中垂线上,BC=6cm,BD=5cm,那么△ABC的周长是6+2$\sqrt{6}$+2$\sqrt{15}$cm.
如图所示,在△ABC中,∠C=90°,D点在线段AB的中垂线上,BC=6cm,BD=5cm,那么△ABC的周长是6+2$\sqrt{6}$+2$\sqrt{15}$cm.