题目内容
 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)△ADF与△DEC相似吗?为什么?
(2)若AB=4,AD=
| 27 |
考点:平行四边形的性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)首先利用已知得出∠AFD=∠C,进而求出△ADF与△DEC相似;
(2)首先利用勾股定理得出DE的长,再利用相似三角形的性质求出AF的长.
(2)首先利用勾股定理得出DE的长,再利用相似三角形的性质求出AF的长.
解答:解:(1)△ADF∽△DEC;
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°,
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=4,
又∵AE⊥BC,∴AE⊥AD,
在Rt△ADE中,DE=
=
=6,
∵△ADF∽△DEC,
∴
=
,
∴
=
,
解得:AF=2
.
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°,
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=4,
又∵AE⊥BC,∴AE⊥AD,
在Rt△ADE中,DE=
| AD2+AE2 |
(3
|
∵△ADF∽△DEC,
∴
| AD |
| DE |
| AF |
| CD |
∴
3
| ||
| 6 |
| AF |
| 4 |
解得:AF=2
| 3 |
点评:此题主要考查了平行四边形的性质以及勾股定理和相似三角形的判定与性质,得出∠AFD=∠C是解题关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
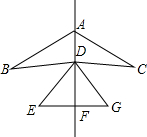 如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )
如图是一个风筝的图案,它是以直线AF为对称轴的轴对称图形,下列结论中不一定成立的是( )| A、△ABD≌△ACD |
| B、AF垂直平分EG |
| C、∠B=∠C |
| D、DE=EG |
下列说法正确的是( )
| A、所有正方形都是全等图形 |
| B、所有长方形都是全等图形 |
| C、所有半径相等的圆都是全等图形 |
| D、面积相等的两个三角形是全等图形 |
 已知,如图在直角坐标系内,矩形OABC,AB=4,BC=2.
已知,如图在直角坐标系内,矩形OABC,AB=4,BC=2.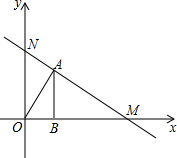 如图,点M的坐标为(13,0),点A在第一象限,AB⊥x轴,垂足为B,tan∠AOB=
如图,点M的坐标为(13,0),点A在第一象限,AB⊥x轴,垂足为B,tan∠AOB=