题目内容
求一切实数k,使关于x的方程:5x2-5kx+66k-1=0的两根均为正整数.
考点:一元二次方程的整数根与有理根,奇数与偶数,数的整除性
专题:探究型
分析:假设方程有两个正整数根,设为x1、x2.根据根与系数的关系可得:x1+x2=k,x1•x2=13k+
,由x1、x2都是正整数可得k、13k+
都是正整数,进而得到
是整数,设
=n,则有k=5n+1,n为整数,由x1+x2=5n+1得到正整数x1与x2一奇一偶,从而有x1•x2是偶数,与x1•x2=66n+13是奇数矛盾,故假设不成立,因而满足要求的实数k不存在.
| k-1 |
| 5 |
| k-1 |
| 5 |
| k-1 |
| 5 |
| k-1 |
| 5 |
解答:解:假设方程有两个正整数根,设为x1、x2.
根据根与系数的关系可得:x1+x2=-
=k,x1•x2=
=13k+
.
∵x1、x2都是正整数,∴k、13k+
都是正整数,
∴
是整数.
设
=n,则有k=5n+1,n为整数,
∴x1+x2=5n+1,n为整数.
∵5n+1(n为整数)是奇数,
∴正整数x1与x2一奇一偶,
∴x1•x2是偶数,
与x1•x2=13(5n+1)+n=66n+13是奇数矛盾.
∴假设不成立.
∴满足要求的实数k不存在.
根据根与系数的关系可得:x1+x2=-
| -5k |
| 5 |
| 66k-1 |
| 5 |
| k-1 |
| 5 |
∵x1、x2都是正整数,∴k、13k+
| k-1 |
| 5 |
∴
| k-1 |
| 5 |
设
| k-1 |
| 5 |
∴x1+x2=5n+1,n为整数.
∵5n+1(n为整数)是奇数,
∴正整数x1与x2一奇一偶,
∴x1•x2是偶数,
与x1•x2=13(5n+1)+n=66n+13是奇数矛盾.
∴假设不成立.
∴满足要求的实数k不存在.
点评:本题考查了一元二次方程正整数解的问题,用到了根与系数的关系、奇数与偶数、数的整除性等知识,而运用反证法是解决本题的关键.

练习册系列答案
相关题目
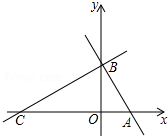 如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2-(
如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2-( 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. 如图,抛物线y=ax2+bx+c与x轴交于(1,0)和(3,0)两点,交y轴与(0,3),当x
如图,抛物线y=ax2+bx+c与x轴交于(1,0)和(3,0)两点,交y轴与(0,3),当x 如图,△ABC≌△DEF,∠A=35°,∠B=55°,求∠DFE的度数.
如图,△ABC≌△DEF,∠A=35°,∠B=55°,求∠DFE的度数.