题目内容
 已知,如图在直角坐标系内,矩形OABC,AB=4,BC=2.
已知,如图在直角坐标系内,矩形OABC,AB=4,BC=2.(1)写出A、B、C三点坐标;
(2)在x轴上存在点M,使得△MAB为等腰三角形,你能写出符合要求的点M的坐标吗?(直接写出坐标即可,不必写出过程);
(3)请你探索一下,在x轴上是否存在点M,使△MAB为等腰直角三角形?
考点:圆的综合题
专题:
分析:(1)根据矩形的性质以及AB,BC的长度即可求出A、B、C三点坐标;
(2)在x轴上存在点M,使得△MAB为等腰三角形,分三种情况分别讨论即MA=MB,MA=AB,MB=AB时求出M的坐标即可;
(3)在x轴上是否存在点M,使△MAB为等腰直角三角形,由(2)可知当M在AB的垂直平分线上时,则△MAB为等腰直角三角形.
(2)在x轴上存在点M,使得△MAB为等腰三角形,分三种情况分别讨论即MA=MB,MA=AB,MB=AB时求出M的坐标即可;
(3)在x轴上是否存在点M,使△MAB为等腰直角三角形,由(2)可知当M在AB的垂直平分线上时,则△MAB为等腰直角三角形.
解答:解:(1)∵四边形AOCB是矩形,
∴OC=AB=4,BC=AO=2,
∴A(0,2),B(4,2),C(4,0);
(2)在x轴上存在点M,使得△MAB为等腰三角形,
理由如下:(如图所示)
当MA=MB,作AB的垂直平分线交x轴于M3,
∵AB=4,
∴OM3=2,
∴M3(2,0);
当AB=MB时,以B为圆心AB长为半径画圆交x轴于M2,M5,
设OM2=x,则CM2=4-x,
在Rt△BM2C中,BM2=4,BC=2,
∴(4-x)2+22=42,
∴x=4+2
或4-2
,
∴M2(4-2
,0),M5(4+2
,0)
同理当AM=AB时,则M1(-2
,0),M4(2
,0)
∴一共有5个点M,使得△MAB为等腰三角形;
(3)在x轴上是否存在点M,使△MAB为等腰直角三角形,
理由如下:
显然A,B不能为直角顶点,所以只能是M为直角顶点,
由(2)可知当AM=BM时,则△AMB是等腰直角三角形,即M3(2,0).
∴OC=AB=4,BC=AO=2,
∴A(0,2),B(4,2),C(4,0);
(2)在x轴上存在点M,使得△MAB为等腰三角形,
理由如下:(如图所示)
当MA=MB,作AB的垂直平分线交x轴于M3,
∵AB=4,
∴OM3=2,
∴M3(2,0);
当AB=MB时,以B为圆心AB长为半径画圆交x轴于M2,M5,

设OM2=x,则CM2=4-x,
在Rt△BM2C中,BM2=4,BC=2,
∴(4-x)2+22=42,
∴x=4+2
| 3 |
| 3 |
∴M2(4-2
| 3 |
| 3 |
同理当AM=AB时,则M1(-2
| 3 |
| 3 |
∴一共有5个点M,使得△MAB为等腰三角形;
(3)在x轴上是否存在点M,使△MAB为等腰直角三角形,
理由如下:
显然A,B不能为直角顶点,所以只能是M为直角顶点,
由(2)可知当AM=BM时,则△AMB是等腰直角三角形,即M3(2,0).
点评:本题考查了矩形的性质、勾股定理的运用、解一元二次方程以及等腰三角形的判定和性质,解题的关键是利用分类讨论的数学方法解决几何问题,特别是找M的位置要充分利用圆的性质做到不重不漏,题目的综合性较强,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图是一均匀薄板,半径R=30cm,现从板上挖掉一个r=15cm的内切圆,试求剩余薄板的重心C与大圆圆心O的距离.
如图是一均匀薄板,半径R=30cm,现从板上挖掉一个r=15cm的内切圆,试求剩余薄板的重心C与大圆圆心O的距离.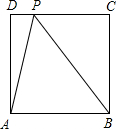 如图,正方形ABCD的边长为4,动点P从D出发以1个单位每秒的速度往C运动,动点Q从A出发以3个单位每秒的速度经B往C运动,若P、Q同时出发,其中一个点运动到C时,另一点也随即停止运动,连结PA、PQ,若记△APQ的面积为y,运动时间为x秒.
如图,正方形ABCD的边长为4,动点P从D出发以1个单位每秒的速度往C运动,动点Q从A出发以3个单位每秒的速度经B往C运动,若P、Q同时出发,其中一个点运动到C时,另一点也随即停止运动,连结PA、PQ,若记△APQ的面积为y,运动时间为x秒. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.