题目内容
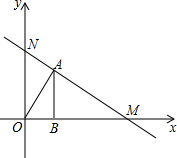 如图,点M的坐标为(13,0),点A在第一象限,AB⊥x轴,垂足为B,tan∠AOB=
如图,点M的坐标为(13,0),点A在第一象限,AB⊥x轴,垂足为B,tan∠AOB=| 3 |
| 2 |
(1)sin∠AOB=
(2)如果△AOM是等腰三角形,求点A的坐标;
(3)设直线MA与y轴相交于点N,以M、O、N为顶点的三角形与△AOB相似的情况是否存在?如果存在,请直接写出点A的坐标;如果不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据锐角三角函数的定义,可得正弦函数值;
(2)分类讨论:OA=AM,AO=OM,MA=OM,根据等腰三角形的性质,可得二元二次方程组,根据解方程组,可得答案;
(3)根据相似三角形的性质,可得
=
,
=
,根据比例的性质,可得
=
=
,
=
,根据解方程组,可得大答案.
(2)分类讨论:OA=AM,AO=OM,MA=OM,根据等腰三角形的性质,可得二元二次方程组,根据解方程组,可得答案;
(3)根据相似三角形的性质,可得
| AB |
| ON |
| OB |
| OM |
| AB |
| OM |
| OB |
| ON |
| ON |
| OM |
| AB |
| OB |
| 3 |
| 2 |
| OM |
| ON |
| AB |
| OB |
解答:解:(1)设点A为(x,y)
因为点A在第一象限,AB⊥x轴
tan∠AOB=
=
①,
y=
x,
OA=
=
x,
ain∠AOB=
=
=
,
故答案为:
;
(2)当AO=AM时,则AO2=AM2,
即x2+y2=(13-x)2+y2 ②
由①②得
,
解得
,
即A(
,
)
当OA=OM时,则MA2=OM2,
即x2+y2=169 ③
由①③得
,
解得
,
即A(2
,3
);
当MA=OM时,则MA2=OM2,
即(13-x)2+y2=169 ④
由①④得
,
解得
,
(不符合题意的要舍去),
即A(8,12),
综上所述:△AOM是等腰三角形,求点A的坐标是(
,
),(2
,3
),(8,12);
(3)存在A点,以M、O、N为顶点的三角形与△AOB相似,
当△OAB∽△MON时,
=
,
=
=
,
ON=
OM=
,N(0,
),
直线MN y=-
x+
④,
由①④得
,
解得
,
A(
,
);
当△OAB∽△NMO时,
=
,
=
,
ON=
•OM=
×13=
,N(0,
),
直线MNy=-
x+
⑤,
由①⑤得
,
解得
,
A(4,6),
综上所述:A(4,6),(
,
)时,以M、O、N为顶点的三角形与△AOB相似.
因为点A在第一象限,AB⊥x轴
tan∠AOB=
| y |
| x |
| 3 |
| 2 |
y=
| 3 |
| 2 |
OA=
| x2+y2 |
| ||
| 2 |
ain∠AOB=
| AB |
| OA |
| ||||
|
3
| ||
| 13 |
故答案为:
3
| ||
| 13 |
(2)当AO=AM时,则AO2=AM2,
即x2+y2=(13-x)2+y2 ②
由①②得
|
解得
|
即A(
| 13 |
| 2 |
| 39 |
| 4 |
当OA=OM时,则MA2=OM2,
即x2+y2=169 ③
由①③得
|
解得
|
即A(2
| 13 |
| 13 |
当MA=OM时,则MA2=OM2,
即(13-x)2+y2=169 ④
由①④得
|
解得
|
|
即A(8,12),
综上所述:△AOM是等腰三角形,求点A的坐标是(
| 13 |
| 2 |
| 39 |
| 4 |
| 13 |
| 13 |
(3)存在A点,以M、O、N为顶点的三角形与△AOB相似,
当△OAB∽△MON时,
| AB |
| ON |
| OB |
| OM |
| ON |
| OM |
| AB |
| OB |
| 3 |
| 2 |
ON=
| 3 |
| 2 |
| 39 |
| 2 |
| 39 |
| 2 |
直线MN y=-
| 3 |
| 2 |
| 39 |
| 2 |
由①④得
|
解得
|
A(
| 13 |
| 2 |
| 39 |
| 4 |
当△OAB∽△NMO时,
| AB |
| OM |
| OB |
| ON |
| OM |
| ON |
| AB |
| OB |
ON=
| OB |
| AB |
| 2 |
| 3 |
| 26 |
| 3 |
| 26 |
| 3 |
直线MNy=-
| 2 |
| 3 |
| 26 |
| 3 |
由①⑤得
|
解得
|
A(4,6),
综上所述:A(4,6),(
| 13 |
| 2 |
| 39 |
| 4 |
点评:本题考查了一次函数的综合题,利用了三角函数的定义,等腰三角形的定义,相似三角形的性质,综合性较强,题目稍有难度.

练习册系列答案
相关题目
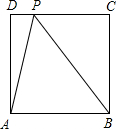 如图,正方形ABCD的边长为4,动点P从D出发以1个单位每秒的速度往C运动,动点Q从A出发以3个单位每秒的速度经B往C运动,若P、Q同时出发,其中一个点运动到C时,另一点也随即停止运动,连结PA、PQ,若记△APQ的面积为y,运动时间为x秒.
如图,正方形ABCD的边长为4,动点P从D出发以1个单位每秒的速度往C运动,动点Q从A出发以3个单位每秒的速度经B往C运动,若P、Q同时出发,其中一个点运动到C时,另一点也随即停止运动,连结PA、PQ,若记△APQ的面积为y,运动时间为x秒.
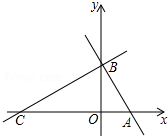 如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2-(
如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2-( 如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的从正面看与从左面看的视图.
如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的从正面看与从左面看的视图. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.