题目内容
3.为了了解2016年我县九年级6023名学生学业水平考试的数学成绩,从中随机抽取了200名学生的数学成绩,下列说法正确的是( )| A. | 2016年我县九年级学生是总体 | |
| B. | 每一名九年级学生是个体 | |
| C. | 200名九年级学生是总体的一个样本 | |
| D. | 样本容量是200 |
分析 分别利用总体以及、样本、样本容量的定义分析得出答案.
解答 解:A、2016年我县九年级学生的数学成绩是总体,故此选项错误,不合题意;
B、每一名九年级学生的数学成绩是个体,故此选项错误,不合题意;
C、200名九年级学生的数学成绩是总体的一个样本,故此选项错误,不合题意;
D、样本容量是200,故此选项正确,符合题意;
故选:D.
点评 此题主要考查了总体、样本、样本容量,正确把握相关定义是解题关键.

练习册系列答案
相关题目
11.下列等式一定成立的是( )
| A. | 2a+3b=5ab | B. | (a3)2=a5 | C. | a2•a3=a5 | D. | (a+b)2=a2+b2 |
18.为了实现街巷硬化工程高质量“全覆盖”,我省今年1-4月公路建设累计投资92.7亿元,该数据用科学记数法可表示为( )
| A. | 0.927×1010 | B. | 92.7×1010 | C. | 9.27×1011 | D. | 9.27×109 |
15.同时抛掷A,B两个均匀的小正方体(每个面上分别标有数字1、2、3、4、5、6),设两个正方体朝上的数字分别是x,y,并以此确定点P(x,y),那么点P落在抛物线y=-x2+3x上的概率是( )
| A. | $\frac{1}{18}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{9}$ |
12.下列计算中,错误的是( )
| A. | -3a+2a=-a | B. | a3•a2=a6 | C. | (3a3)2=9a6 | D. | 6a2b÷3b=2a2 |
13.要使代数式$\frac{\sqrt{x+1}}{x}$有意义,则实数x的取值范围是( )
| A. | x≥1 | B. | x≥-1 | C. | x≥-1且x≠0 | D. | x>-1且x≠0 |
 如图,在?ABCD的对角线BD上取一点E,使得BE=$\frac{1}{4}$BD,延长AE交BC于G,交DC的延长线于F,求:S△CFG:S△BEG的值.
如图,在?ABCD的对角线BD上取一点E,使得BE=$\frac{1}{4}$BD,延长AE交BC于G,交DC的延长线于F,求:S△CFG:S△BEG的值.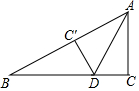 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=15,点D是BC边上一点,连接AD,将△ABC沿AD折叠,点C恰好落在边AB上的点C′处,则CD的长是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=15,点D是BC边上一点,连接AD,将△ABC沿AD折叠,点C恰好落在边AB上的点C′处,则CD的长是$\frac{24}{5}$. 如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(阴影部分)的面积之和是10πcm2.
如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,则图中三个扇形(阴影部分)的面积之和是10πcm2.