题目内容
14.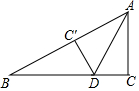 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=15,点D是BC边上一点,连接AD,将△ABC沿AD折叠,点C恰好落在边AB上的点C′处,则CD的长是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=15,点D是BC边上一点,连接AD,将△ABC沿AD折叠,点C恰好落在边AB上的点C′处,则CD的长是$\frac{24}{5}$.
分析 先依据勾股定理求得AB的长,然后依据翻折的性质得到AC′=8,设DC′=CD=x,最后在Rt△BC′D中,依据勾股定理求解即可.
解答 解:在Rt△ABC中,依据勾股定理可知AB=$\sqrt{A{C}^{2}+C{B}^{2}}$=$\sqrt{1{5}^{2}+{8}^{2}}$=17.
由翻折的性质可知AC=AC′=8,DC=DC′=x,则BC′=9,BD=15-x.
在Rt△ABC中,依据勾股定理得:BD2=DC′2+BC′2,即(15-x)2=x2+92,
解得:x=$\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 本题主要考查的是勾股定理和翻折的性质,熟练掌握勾股定理和翻折的性质是解题的关键.

练习册系列答案
相关题目
2.若函数y=(k+2)x+b-1是一次函数,则( )
| A. | k≠0,b≠1 | B. | k≠-2,b≠1 | C. | k≠0,b为任意数 | D. | k≠-2,b为任意数 |
6.使二次根式$\sqrt{x-2}$有意义的x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x<2 | D. | x>-2 |
3.为了了解2016年我县九年级6023名学生学业水平考试的数学成绩,从中随机抽取了200名学生的数学成绩,下列说法正确的是( )
| A. | 2016年我县九年级学生是总体 | |
| B. | 每一名九年级学生是个体 | |
| C. | 200名九年级学生是总体的一个样本 | |
| D. | 样本容量是200 |
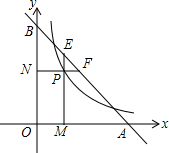 如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=$\frac{k}{x}$(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于AB于点F,且AF•BE=8,则k=4.
如图,直线y=6-x交x轴、y轴于A、B两点,P是反比例函数y=$\frac{k}{x}$(x>0)图象上位于直线下方的一点,过点P作x轴的垂线,垂足为点M,交AB于点E,过点P作y轴的垂线,垂足为点N,交AB于AB于点F,且AF•BE=8,则k=4.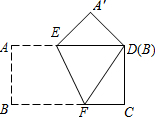 把一张矩形纸片ABCD按如图所示的方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图所示的方式折叠,使顶点B和D重合,折痕为EF.