题目内容
15.同时抛掷A,B两个均匀的小正方体(每个面上分别标有数字1、2、3、4、5、6),设两个正方体朝上的数字分别是x,y,并以此确定点P(x,y),那么点P落在抛物线y=-x2+3x上的概率是( )| A. | $\frac{1}{18}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{9}$ |
分析 画树状图展示所有36种等可能的结果数,再根据二次函数图象上点的坐标特征得到点(1,2),(2,2)在抛物线y=-x2+3x上,然后根据概率公式求解即可.
解答 解:画树状图为:
共有36种等可能的结果数,其中点(1,2),(2,2)在抛物线y=-x2+3x上,
所以点P在抛物线y=-x2+3x上的概率=$\frac{2}{36}$=$\frac{1}{18}$.
故选A.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
6.使二次根式$\sqrt{x-2}$有意义的x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x<2 | D. | x>-2 |
3.为了了解2016年我县九年级6023名学生学业水平考试的数学成绩,从中随机抽取了200名学生的数学成绩,下列说法正确的是( )
| A. | 2016年我县九年级学生是总体 | |
| B. | 每一名九年级学生是个体 | |
| C. | 200名九年级学生是总体的一个样本 | |
| D. | 样本容量是200 |
10.-$\frac{1}{3}$的相反数是( )
| A. | -3 | B. | $\frac{1}{3}$ | C. | 3 | D. | -$\frac{1}{3}$ |
20.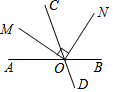 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM.若∠AOC=70°,则∠CON的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
7.下列命题正确是( )
| A. | 点(1,3)关于x轴的对称点是(-1,3) | |
| B. | 函数 y=-2x+3中,y随x的增大而增大 | |
| C. | 若一组数据3,x,4,5,6的众数是3,则中位数是3 | |
| D. | 同圆中的两条平行弦所夹的弧相等 |
5.a(a≠0)的相反数是( )
| A. | -a | B. | a | C. | |a| | D. | $\frac{1}{a}$ |
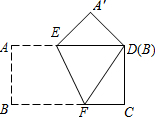 把一张矩形纸片ABCD按如图所示的方式折叠,使顶点B和D重合,折痕为EF.
把一张矩形纸片ABCD按如图所示的方式折叠,使顶点B和D重合,折痕为EF.