题目内容
 如图,锐角△ABC中,以BC为直径的半圆分别交AB,AC于点D,E,记△ADE的面积为S1,△ABC的面积为S2,则
如图,锐角△ABC中,以BC为直径的半圆分别交AB,AC于点D,E,记△ADE的面积为S1,△ABC的面积为S2,则 =
=
- A.sinA
- B.sin2A
- C.cosA
- D.cos2A
D
分析:如图,连接BE.构建直角△ABE,通过解该直角三角形求得cosA= ;然后通过相似三角形△AED∽△ABC的对应边的比成比例知
;然后通过相似三角形△AED∽△ABC的对应边的比成比例知 =
= ;最后结合三角形的面积公式分别求得△ADE、△ABC的面积.
;最后结合三角形的面积公式分别求得△ADE、△ABC的面积.
解答: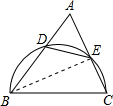 解:如图,连接BE.
解:如图,连接BE.
∵BC为半圆的直径,
∴∠BEC=∠AEB=90°.
∴在直角△ABE中,cosA= ,
,
∵点D、B、C、E四点共圆,
∴∠ABC+∠DEC=180°.
∵∠DEC+∠AED=180°,
∴∠ABC=∠AED.
又∵∠A=∠A,
∴△AED∽△ABC,
∴ =
= .
.
∵S1= AE•AD•sinA,S2=
AE•AD•sinA,S2= AB•AC•sinA,
AB•AC•sinA,
 =
=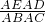 =
=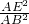 =cos2A.
=cos2A.
故选D.
点评:本题考查了相似三角形的判定与性质、圆周角定理以及解直角三角形等知识点.解答该题时,借用了圆内接四边形的内对角互补的性质.
分析:如图,连接BE.构建直角△ABE,通过解该直角三角形求得cosA=
 ;然后通过相似三角形△AED∽△ABC的对应边的比成比例知
;然后通过相似三角形△AED∽△ABC的对应边的比成比例知 =
= ;最后结合三角形的面积公式分别求得△ADE、△ABC的面积.
;最后结合三角形的面积公式分别求得△ADE、△ABC的面积.解答:
 解:如图,连接BE.
解:如图,连接BE.∵BC为半圆的直径,
∴∠BEC=∠AEB=90°.
∴在直角△ABE中,cosA=
 ,
,∵点D、B、C、E四点共圆,
∴∠ABC+∠DEC=180°.
∵∠DEC+∠AED=180°,
∴∠ABC=∠AED.
又∵∠A=∠A,
∴△AED∽△ABC,
∴
 =
= .
.∵S1=
 AE•AD•sinA,S2=
AE•AD•sinA,S2= AB•AC•sinA,
AB•AC•sinA, =
=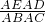 =
=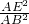 =cos2A.
=cos2A.故选D.
点评:本题考查了相似三角形的判定与性质、圆周角定理以及解直角三角形等知识点.解答该题时,借用了圆内接四边形的内对角互补的性质.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 如图,锐角△ABC中,PQRS是△ABC的内接矩形,且S△ABC=nS矩形PQRS,其中n为不小于3的自然数.求证:
如图,锐角△ABC中,PQRS是△ABC的内接矩形,且S△ABC=nS矩形PQRS,其中n为不小于3的自然数.求证: 如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值. 10、如图,锐角△ABC中,AD和CE分别是BC和AB边上的高,若AD与CE所夹的锐角是58°,则∠BAC+∠BCA的大小是
10、如图,锐角△ABC中,AD和CE分别是BC和AB边上的高,若AD与CE所夹的锐角是58°,则∠BAC+∠BCA的大小是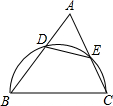 (1997•浙江)如图,锐角△ABC中,以BC为直径的半圆分别交AB,AC于点D,E,记△ADE的面积为S1,△ABC的面积为S2,则
(1997•浙江)如图,锐角△ABC中,以BC为直径的半圆分别交AB,AC于点D,E,记△ADE的面积为S1,△ABC的面积为S2,则 如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,那么∠ACB与∠DFE 的关系是( )
如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,那么∠ACB与∠DFE 的关系是( )