题目内容
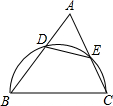（1997•浙江）如图，锐角△ABC中，以BC为直径的半圆分别交AB，AC于点D，E，记△ADE的面积为S1，△ABC的面积为S2，则| S1 |
| S2 |
分析：如图，连接BE．构建直角△ABE，通过解该直角三角形求得cosA=
；然后通过相似三角形△AED∽△ABC的对应边的比成比例知
=
；最后结合三角形的面积公式分别求得△ADE、△ABC的面积．
| AE |
| AB |
| AE |
| AB |
| AD |
| AC |
解答：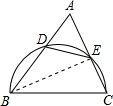
解：如图，连接BE．
∵BC为半圆的直径，
∴∠BEC=∠AEB=90°．
∴在直角△ABE中，cosA=
，
∵点D、B、C、E四点共圆，
∴∠ABC+∠DEC=180°．
∵∠DEC+∠AED=180°，
∴∠ABC=∠AED．
又∵∠A=∠A，
∴△AED∽△ABC，
∴
=
．
∵S1=
AE•AD•sinA，S2=
AB•AC•sinA，
=
=
=cos2A．
故选D．
解：如图，连接BE．∵BC为半圆的直径，
∴∠BEC=∠AEB=90°．
∴在直角△ABE中，cosA=
| AE |
| AB |
∵点D、B、C、E四点共圆，
∴∠ABC+∠DEC=180°．
∵∠DEC+∠AED=180°，
∴∠ABC=∠AED．
又∵∠A=∠A，
∴△AED∽△ABC，
∴
| AE |
| AB |
| AD |
| AC |
∵S1=
| 1 |
| 2 |
| 1 |
| 2 |
| S1 |
| S2 |
| AE•AD |
| AB•AC |
| AE2 |
| AB2 |
故选D．
点评：本题考查了相似三角形的判定与性质、圆周角定理以及解直角三角形等知识点．解答该题时，借用了圆内接四边形的内对角互补的性质．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
（1997•浙江）如图，矩形ABCD中，AB=3，BC=4，线段EF在对角线AC上，EG⊥AD，FH⊥BC，垂足分别是G，H，且EG+FH=EF．
（1997•浙江）如图，?ABCD中，对角线AC和BD交于点O，过O作OE∥BC交DC于点E，若OE=5cm，则AD的长为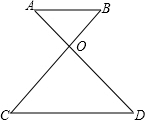
（1997•浙江）如图，AB∥CD，AD和BC交于点O，若∠A=42°，∠C=51°，则∠AOB=（ ）
（1997•浙江）如图，⊙O1与⊙O2相交，大圆⊙O1的弦AB⊥O1O2，垂足是F，且交⊙O2于点C，D，过B作⊙O2的切线，E为切点，已知BE=DE，BD=m，BE=n，AC，CE的长是关于x的方程x2+px+q=0的两个根．