题目内容
 10、如图,锐角△ABC中,AD和CE分别是BC和AB边上的高,若AD与CE所夹的锐角是58°,则∠BAC+∠BCA的大小是
10、如图,锐角△ABC中,AD和CE分别是BC和AB边上的高,若AD与CE所夹的锐角是58°,则∠BAC+∠BCA的大小是122°
.分析:根据直角三角形的两个锐角互余,求得∠BAD=∠BCE=90°-58°=32°,根据三角形的外角的性质,求得∠DAC+∠DCA=58°,从而求解.
解答:解:∵AD和CE分别是BC和AB边上的高,
∴∠BAD=∠BCE=90°-58°=32°,
又∠DAC+∠DCA=58°,
∴∠BAC+∠BCA=32°×2+58°=122°.
故答案为122°.
∴∠BAD=∠BCE=90°-58°=32°,
又∠DAC+∠DCA=58°,
∴∠BAC+∠BCA=32°×2+58°=122°.
故答案为122°.
点评:此题综合运用了三角形的内角和定理的推论:直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
相关题目
 如图,锐角△ABC中,PQRS是△ABC的内接矩形,且S△ABC=nS矩形PQRS,其中n为不小于3的自然数.求证:
如图,锐角△ABC中,PQRS是△ABC的内接矩形,且S△ABC=nS矩形PQRS,其中n为不小于3的自然数.求证: 如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.
如图,锐角△ABC中,AB=10cm,BC=9cm,△ABC的面积为27cm2.求tanB的值.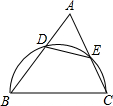 (1997•浙江)如图,锐角△ABC中,以BC为直径的半圆分别交AB,AC于点D,E,记△ADE的面积为S1,△ABC的面积为S2,则
(1997•浙江)如图,锐角△ABC中,以BC为直径的半圆分别交AB,AC于点D,E,记△ADE的面积为S1,△ABC的面积为S2,则 如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,那么∠ACB与∠DFE 的关系是( )
如图,锐角△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,那么∠ACB与∠DFE 的关系是( )