题目内容
14.将二次函数y=-x2+2的图象绕原点旋转180°,得到一条新的二次函数的图象,则这个二次函数的函数表达式为y=x2+2.分析 先利用顶点式得到抛物线y=-x2+2的顶点坐标为(0,2),再根据旋转的性质得到旋转后的抛物线顶点坐标为(0,2),二次项系数为1,由此根据顶点式可写出旋转后的抛物线解析式.
解答 解:抛物线y=-x2+2的顶点坐标为(0,2),
因为二次函数y=x2+2的图象绕原点旋转180°后得到的抛物线顶点坐标不变,只是开口方向相反,
所以旋转后的抛物线解析式为y=x2+2.
故答案为y=x2+2.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
7.下列多项式乘法中,不能用平方差公式计算的是( )
| A. | (x-y)(-x-y) | B. | (-x2-y2)(y2-x2) | C. | (x3-y3)(x3+y3) | D. | (x-y)(y-x) |
4.在同圆中,圆心角∠AOB=2∠COD,则两条弦AB与CD关系是( )
| A. | AB=2CD | B. | AB=CD | C. | AB<2CD | D. | AB>2CD |
 按如图样式在日历上用一个斜框框出三个数,若三个数和为51,则这三天中的第一天是这个月的9号.
按如图样式在日历上用一个斜框框出三个数,若三个数和为51,则这三天中的第一天是这个月的9号.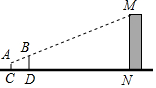 小亮想借助标杆测量教学楼的高度,他采用了下面的方法,先在楼前距离点N57m处直立一根高2m的标杆BD,然后他往后退,退到距离标杆3m的C处(点C,D,N在一条直线上)蹲下,通过调整眼睛离地面的高度,当楼的顶部M,标杆的顶部B及他的眼睛A恰好在同一条直线上时,让同伴量出眼睛与地面的距离AC为1m,根据上面的数据.你能帮小亮求出教学楼的高度吗?
小亮想借助标杆测量教学楼的高度,他采用了下面的方法,先在楼前距离点N57m处直立一根高2m的标杆BD,然后他往后退,退到距离标杆3m的C处(点C,D,N在一条直线上)蹲下,通过调整眼睛离地面的高度,当楼的顶部M,标杆的顶部B及他的眼睛A恰好在同一条直线上时,让同伴量出眼睛与地面的距离AC为1m,根据上面的数据.你能帮小亮求出教学楼的高度吗?