题目内容
4.在同圆中,圆心角∠AOB=2∠COD,则两条弦AB与CD关系是( )| A. | AB=2CD | B. | AB=CD | C. | AB<2CD | D. | AB>2CD |
分析 根据角平分线的性质得出∠AOE=∠EOB,进而利用圆心角与弧的关系可直接求解.
解答  解:作∠AOB的角平分线OE,
解:作∠AOB的角平分线OE,
∵OE平分∠AOB,
∴∠AOE=∠EOB,
∵∠AOB=2∠COD,
∴∠AOE=∠EOB=∠COD,
∴$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$,
∴$\widehat{AB}$=2$\widehat{CD}$,
∴AB=2CD.
故选:A.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列命题中,是真命题的是( )
| A. | 相等的角是对顶角 | B. | 两直线平行,内错角相等 | ||
| C. | 两个锐角的和是锐角 | D. | 互补的角是邻补角 |
9.若某商品的原价为100元,连续两次涨价后的售价为144元,设两次平增长率为x.则下面所列方程正确的是( )
| A. | 100(1-x)2=144 | B. | 100(1+x)2=144 | C. | 100(1-2x)2=144 | D. | 100(1-x)2=144 |
14.下列各式中,不是整式的是( )
| A. | 6ab | B. | $\frac{b}{a}$ | C. | a+1 | D. | 0 |
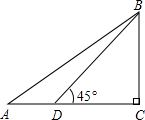 如图,在△ABC,∠C=90°,sin A=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,BD=6$\sqrt{2}$,求AB的长.
如图,在△ABC,∠C=90°,sin A=$\frac{2}{5}$,D为AC上一点,∠BDC=45°,BD=6$\sqrt{2}$,求AB的长.