题目内容
12.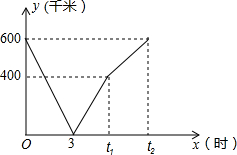 一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,则t2-t1的值为2.5小时.
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系,则t2-t1的值为2.5小时.
分析 根据函数的图象得到600千米的路程两车3小时相遇,于是求得两车的速度和为200km/h,由于相遇后经过2h两车相距400km,求出t1=3+$\frac{400}{200}$=5h,根据慢车3h走的路程快车2h走完,于是得到快车和慢车的速度比为3:2,求出快车的速度为120km/h,慢车的速度为80km/h,即可得到结论.
解答 解:∵600千米的路程两车3小时相遇,
∴两车的速度和为200km/h,
∴相遇后经过2h两车相距400km,
∴t1=3+$\frac{400}{200}$=5h,
∵慢车3h走的路程快车2h走完,
∴快车和慢车的速度比为3:2,
∴快车的速度为120km/h,慢车的速度为80km/h,
∴120×3÷80=4.5,
∴t2=3+4.5=7.5,
∴t2-t1=7.5-5=2.5,
故答案为:2.5.
点评 此题主要考查了一次函数的应用,利用图表中数据得出慢车速度是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.一次奥运知识竞赛中,一共有25道题,答对一题得10分,答错(或不答)一题扣5分.设小明同学在这次竞赛中答对x道题.
(1)根据所给条件,完成下表:
(2)若小明同学的竞赛成绩为205分,则他答对几道题?
(1)根据所给条件,完成下表:
| 答题情况 | 答对 | 答错或不答 |
| 题数 | x | 25-x |
| 每题分值 | 10 | -5 |
| 得分 | 10x | -5(25-x) |
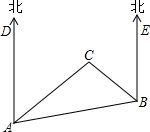 如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?
如图,是A、B、C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西30°方向,从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢?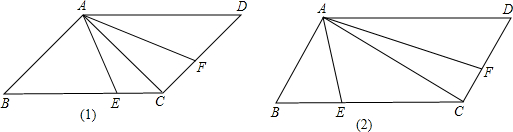
 如图,已知A(1,3),B(5,0),在x轴上是否存在点P,使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
如图,已知A(1,3),B(5,0),在x轴上是否存在点P,使△PAB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.