题目内容
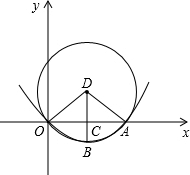 ⊙O经过坐标原点,且与x轴交于点A、DC⊥x轴于点C,且与⊙D交于点B,已知⊙D的半径为2
⊙O经过坐标原点,且与x轴交于点A、DC⊥x轴于点C,且与⊙D交于点B,已知⊙D的半径为2| 3 |
(1)求B点的坐标;
(2)求经过O、B、A三点的抛物线的解析式;
(3)在抛物线上是否存在一点P,使△PAO和△OBA相似?若有,求出P点坐标;不存在,说明理由.
考点:圆的综合题
专题:综合题
分析:(1)根据垂径定理.由DC⊥OA得到OC=AC,再根据等腰三角形的性质由DA=DO,∠ODA=120°得到∠DOC=30°,则可计算出DC=
OD=
,OC=
DC=3,所以CB=DB-DC=
,于是可得到B点坐标为(3,-
);
(2)由于OC=AC=3,则A点坐标为(6,0),设交点式,利用待定系数法求出经过O、B、A三点的抛物线的解析式;
(3)先证明△DOB和△DAB都是等边三角形,则BO=BA,∠ABO=120°,所以∠BOA=∠BAO=30°,若△PAO和△OBA相似,则∠PAO=∠ABO=120°,∠POA=∠BOA=30°,作PH⊥x轴于H,如图,可计算出∠PAH=60°,在Rt△PAH中利用∠APH=30°,AP=AO=6可计算出AH=
PA=3,PH=
AH=3
,则P点坐标为(9,3
)
然后利用抛物线的对称性点(-3,3
)也满足要求,于是得到满足条件的P点坐标为(9,3
)或(-3,3
).
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
(2)由于OC=AC=3,则A点坐标为(6,0),设交点式,利用待定系数法求出经过O、B、A三点的抛物线的解析式;
(3)先证明△DOB和△DAB都是等边三角形,则BO=BA,∠ABO=120°,所以∠BOA=∠BAO=30°,若△PAO和△OBA相似,则∠PAO=∠ABO=120°,∠POA=∠BOA=30°,作PH⊥x轴于H,如图,可计算出∠PAH=60°,在Rt△PAH中利用∠APH=30°,AP=AO=6可计算出AH=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
然后利用抛物线的对称性点(-3,3
| 3 |
| 3 |
| 3 |
解答:解:(1)∵DC⊥OA,
∴OC=AC,
∵DA=DO,∠ODA=120°,
∴∠DOC=30°,
在Rt△ODC中,∵OD=2
,
∴DC=
OD=
,
∴OC=
DC=3,
∴CB=DB-DC=2
-
=
,
∴B点坐标为(3,-
);
(2)∵OC=AC=3,
∴A点坐标为(6,0),
设经过O、B、A三点的抛物线的解析式为y=ax(x-6),
把B(3,-
)代入得a•3•(3-6)=-
,解得a=
,
∴经过O、B、A三点的抛物线的解析式为y=
x(x-6)=
x2-
x;
(3)存在.
∵∠ODB=∠ADB=60°,
∴△DOB和△DAB都是等边三角形,
∴BO=BA,∠ABO=60°+60°=120°,
∴∠BOA=∠BAO=30°,
∵△PAO和△OBA相似,
∴∠PAO=∠ABO=120°,∠POA=∠BOA=30°,
作PH⊥x轴于H,如图,
∵∠PAO=120°,
∴∠PAH=60°,
在Rt△PAH中,∵∠APH=30°,AP=AO=6,
∴AH=
PA=3,PH=
AH=3
,
∴P点坐标为(9,3
)
点(9,3
)关于直线x=3的对称点(-3,3
)也满足要求,
∴满足条件的P点坐标为(9,3
)或(-3,3
).
∴OC=AC,
∵DA=DO,∠ODA=120°,
∴∠DOC=30°,
在Rt△ODC中,∵OD=2
| 3 |
∴DC=
| 1 |
| 2 |
| 3 |
∴OC=
| 3 |
∴CB=DB-DC=2
| 3 |
| 3 |
| 3 |
∴B点坐标为(3,-
| 3 |
(2)∵OC=AC=3,
∴A点坐标为(6,0),
设经过O、B、A三点的抛物线的解析式为y=ax(x-6),
把B(3,-
| 3 |
| 3 |
| ||
| 9 |
∴经过O、B、A三点的抛物线的解析式为y=
| ||
| 9 |
| ||
| 9 |
2
| ||
| 3 |
(3)存在.

∵∠ODB=∠ADB=60°,
∴△DOB和△DAB都是等边三角形,
∴BO=BA,∠ABO=60°+60°=120°,
∴∠BOA=∠BAO=30°,
∵△PAO和△OBA相似,
∴∠PAO=∠ABO=120°,∠POA=∠BOA=30°,
作PH⊥x轴于H,如图,
∵∠PAO=120°,
∴∠PAH=60°,
在Rt△PAH中,∵∠APH=30°,AP=AO=6,
∴AH=
| 1 |
| 2 |
| 3 |
| 3 |
∴P点坐标为(9,3
| 3 |
点(9,3
| 3 |
| 3 |
∴满足条件的P点坐标为(9,3
| 3 |
| 3 |
点评:本题考查了圆的综合题:熟练掌握垂径定理、等腰三角形的性质和相似三角形的判定与性质;会利用待定系数法求抛物线解析式;记住含30度的直角三角形三边的关系;理解坐标与图形性质.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
下列“表情图”中,属于轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 实数a,b在数轴上对应点的位置如图所示,则下列结论正确的是( )
实数a,b在数轴上对应点的位置如图所示,则下列结论正确的是( )| A、a+b>0 | ||
| B、a-b<0 | ||
| C、ab>0 | ||
D、
|
 如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC的大小为( )
如图,点O在△ABC内,且到三边的距离相等,若∠A=60°,则∠BOC的大小为( )| A、135° | B、120° |
| C、90° | D、60° |
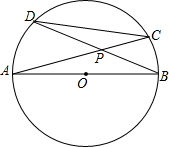 如图,⊙O的直径AB,CD是⊙O的弦,AC与BD相交于点P,若∠BPC=30°,CD=4,求AB.
如图,⊙O的直径AB,CD是⊙O的弦,AC与BD相交于点P,若∠BPC=30°,CD=4,求AB.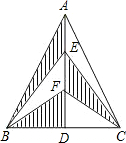 如图,△ABC中,AB=AC,AD⊥BC,点E、F是AD的三等分点,若S△ABC=12m2,则S阴影=
如图,△ABC中,AB=AC,AD⊥BC,点E、F是AD的三等分点,若S△ABC=12m2,则S阴影=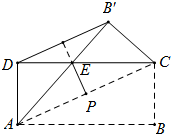 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD相交于点E,连接B′D.若P为AC的中点,求证:PE⊥B′D.